はじめまして。
受験Dr.算数科講師の千葉　誠と申します。

 

東京・神奈川の中学入試解禁日である2月1日が1週間後に迫ってまいりました。

 

受験生の皆さんは日々勉強に励み、様々な問題の解法や知識を学習していることでしょう。
しかし実際のテストや入試問題では、どの解法・知識を利用すればよいのか思いつくことができずに苦戦することが多々あります。

 

そこで今回は平面図形の角度の問題をテーマに、今日から使える2つのコツについてお話しさせていただきます。

 

角度の問題では「やってることは簡単だけど、解き方に気づくのが難しい」と言うお子様が多くいらっしゃいます。

 

このようなお悩みを持つ方に身に着けてほしいコツが２つあります。
１　「わかったことをどんどん書き込む」
２　「作問者の意図を考える」
というものです。

 

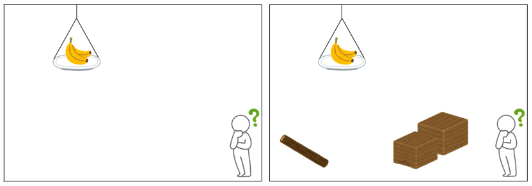
次の絵を見てみてください。

 

 

1枚目は「バナナが手の届かないところにある」という状況です。
2枚目を見たときに「箱にのぼり、棒を使ってバナナを取る」ということが思い浮かんだのではないでしょうか。
つまりこれは「どうやってバナナを取るか」という問題であり、2枚目では「箱」と「棒」がバナナを取るために用意されているという意図を読み取れたわけです。

 

2枚目の状態であればこの問題は非常に簡単と言えます。
「箱」と「棒」が分かりやすく置かれていて、その使い方も明確だからです。

 

当たり前ですが、算数では解決可能な問題しかないため、必要な情報が必ず問題中に用意されています。
しかし難しい問題では、その情報を見つけにくくし、使い方を分かりにくくする工夫がされているのです。

 

そこで、「わかったことをどんどん書き込む」ことで情報が明確になり、「作問者の意図を考える」ことでその情報の使い方がひらめきやすくなるのです。

 

実際の入試問題を見てみましょう。

 

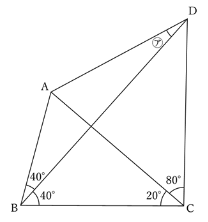
【問題】早稲田中学2020年第2回より抜粋

 

図の四角形ABCDにおいて、角㋐の大きさは何度ですか。

 

 

【解説】
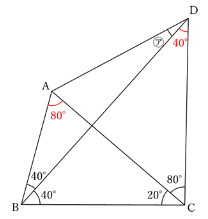
三角形の内角の和は180°であることから
角BDC＝180-(40+20+80)＝40°
角BAC＝180-(40+40+20)＝80°
がすぐわかると思います。
わかったことはどんどん書き込んでいきましょう。

 

 

ここで作問者の意図を考えてみましょう。
書き込んだ角度は「すぐわかるけど図に書かれていない角度」ですので、「作問者が隠したかったヒント」と考えることができます。
そこで、書き込んだ角BDC＝40°について考えてみましょう。
この角度は無作為に決められたわけではなく、作問者が意図的に設定したものです。
この問題において「作問者の意図を考える」とは、「なぜこの角はこの大きさに設定されているのか」を考えるということです。
角BDCはなぜ40°に設定されたのか、40°であることで何が起きるのかを考えると、
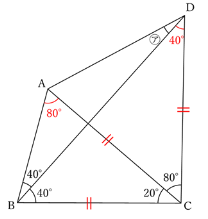
角BDC＝40°＝角DBCなので、
三角形BCDが二等辺三角形になっていることに気づきます。
同様に、書き込んだ角BAC＝80°について考えると、
角BAC＝80°＝角ABCなので、
三角形ABCも二等辺三角形であることがわかります。
このことから
AC＝DC、AC＝BC→AC＝BC＝DC
がわかります。
これも書き込んでみましょう。

 

 

書き込むことでAC＝DCが明確になり、すぐに三角形ACDが二等辺三角形であることがわかります。
よって
角ADC＝(180-80)÷2＝50°
㋐＝50-40＝10°
となります。

 

このようにまず図に書き込んでいくことで情報を明確にする。
そして作問者が何のためにその情報を用意したのかを考えることが解法に気づくコツになります。

 

皆さんもこの2つのコツを身につけて、ぜひ入試本番にお役立てください。

 

それでは、失礼いたします。