こんにちは。
受験Dr.算数科講師の千葉　誠と申します。

今回は「立体図形」と「グラフ」の複合単元である「水量変化とグラフ」テーマに、難問をスラスラ解くための「正面図」の使い方について解説いたします。

ほとんどの生徒は「水量変化とグラフの問題は正面図を書こう」と意識できているのでとりあえず正面図を書いてはくれるのですが、書いたあとどう使えば良いかいまいち分かっておらず、「正面図」を書くだけで止まってしまうといったことが多いです。

今回、実際の入試問題を扱って正面図の正しい使い方とその威力を体感して頂こうと思います。

【問題】（渋谷教育学園幕張中学2024年度入試問題より抜粋）
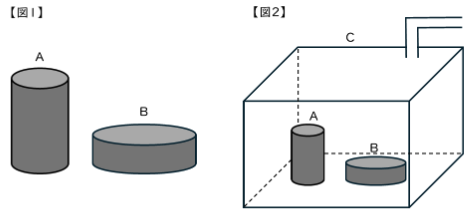
【図１】のように、２つの円柱の形をしたおもりA、Bがあります。AとBの体積は等しく、Ａの高さはＢの高さの3倍です。
【図２】のように、四角柱の形をした空の容器Ｃの中に、おもりＡ、Ｂを置きます。

容器Ｃの中に、１秒あたり同じ量の水を静かに入れ続けたとき、水を入れ始めてからの時間と、容器Ｃの底面から水面までの高さの関係は、下のグラフのようになりました。

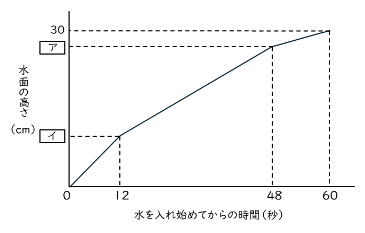
グラフの ア 、 イ にあてはまる数を答えなさい。

【解説】
まずは「正面図」を書いてみましょう。
ここで２つポイントです。
・「おもりは高い順に左に寄せて書く」
・「水の入る順に部屋分けする」

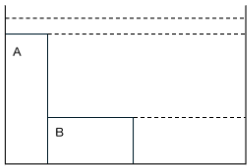
おもりが高い順に端に寄っていないとうまく部屋分けが出来ないので注意しましょう。
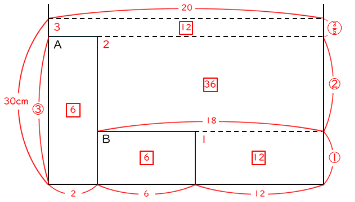
次に、問題設定とグラフの情報を正面図のなかに書き入れていきます。

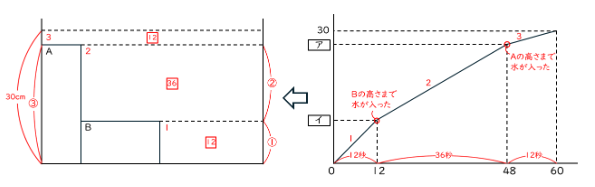
正面図の各部屋の左上の数字は水が入った順番を表しています。
☐で書いてある値はその部屋を満水にするのにかかった時間（秒）ですが、この問題では常に一定の割合で水を入れているので、毎秒 １ の水を入れていると考えると、☐で書いた値はその部屋の体積を表すことになります。
このことから、「正面図」内では「かかった時間を体積として扱う」ことが可能となります。
「時間⇒体積」の置き換えは水量変化の問題をよりシンプルに解くうえで大事なポイントなので覚えておきましょう。
「Ａの高さはＢの高さの3倍」なので、Aの高さを③、Bの高さを①としました。
すると「２の部屋」の高さは②となります。
体積と高さを設定できたので、続いて底面積を考えていきます。
「１の部屋」に注目すると、体積が１２、高さが１なので
１２÷１＝１２・・・「１の部屋」の底面積
「２の部屋」に注目すると、体積が３６、高さが２なので
３６÷２＝１８・・・「２の部屋」の底面積
１８－１２＝６・・・Bの底面積
６×１＝６・・・Bの体積
「AとBの体積は等しい」のでAの体積も６
Aの高さは３なので
６÷３＝２・・・Aの底面積
２＋６＋１２＝２０・・・「３の部屋」の底面積
「３の部屋」の体積は１２なので
１２÷２０＝ ・・・「３の部屋」の高さ

求めた情報を「正面図」に書き加えました。
ここで意識してもらいたいポイントは、
「正面図」では、「横の長さ（底辺）は底面積を表し、面積（底辺×高さ）は体積を表す」ということです。
奥行きが省略されていることによって、
「底辺⇒底面積」、「面積⇒体積」という置き換えが可能となり、簡単な計算で体積、底面積、高さを出していくことができます。
最後に、高さに注目すると
１＋２＋＝3・・・３０cm
３０÷3＝cm・・・Bの高さ
253×３＝２５cm・・・Aの高さ
よって、 ア ＝２５、 イ ＝　が答えとなります。

「正面図」が正しく使えれば、作業は「体積＝底面積×高さ」を利用した計算だけでした。
手順としては、
・「おもりは高い順に左に寄せて書く」
・「水の入る順に部屋分けする」
以上の点に注意して正面図を書き、
・「時間⇒体積」、「底辺⇒底面積」、「面積⇒体積」
この置き換えを使ってすべての部屋の体積、底面積、高さを求めていきました。
これらのポイントを意識して「正面図」を上手く使って解けば、以前は難しく感じた問題も、スラスラ解けると思います。
ぜひ参考にしてみてください。

以上、最後までお読みいただきありがとうございました。
それでは失礼いたします。