こんにちは。
受験Dr.算数科講師の千葉　誠と申します。

今回は、「正三角形の転がり移動」の問題を扱います。
「転がり移動」の問題を解くためには作図が必須ですが、作図は算数で求められる技能の中でも特に得手不得手の差が出やすい部分だと思います。
作図が苦手な生徒は、作図の際に、どういったポイントに注意すべきかを意識できていないためにミスする確率が高くなってしまっている場合が多いです。
今回「作図の注意ポイント」を２つ紹介するので、作図問題でどうしてもミスが出てしまう生徒は必ず身につけておきましょう。

問題

下の図のように，1辺6cmの正三角形PQRが折れ線ABCDEF上にあります。正三角形PQRを折れ線にそって，図のアの位置からイの位置まで,矢印の方向にすべることなく転がします。

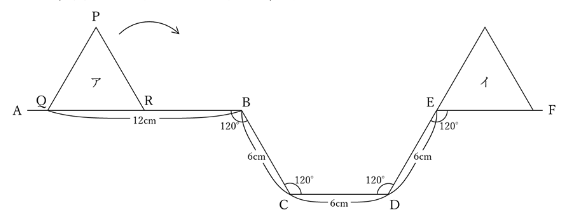
頂点Qが動いたあとの線の長さは何cmですか。ただし、円周率は3.14とします。

解説

まず、正三角形の辺が折れ線に接するときの位置に正三角形を書き入れていきます。
ここで1つ目のポイントです。
・各位置の図形の内側に頂点記号を書き入れる

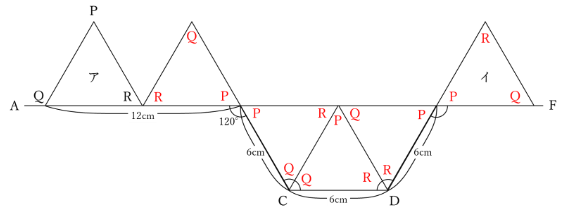
頂点を書き入れておくことで、頂点の動いたあとを書くときのミスがかなり減ります。
記号が密集して頂点を見間違うのを防ぐために、頂点の記号は正三角形の内側に書き込むようにします。
次に、QとQをおうぎ形の弧の線で結んで動いたあとを書いていきますが、ここで2つ目のポイントです。
・回転の中心と半径を確認し、回転角を書き入れる

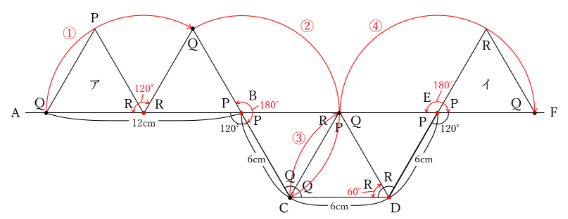
転がり移動は、頂点を中心とする回転移動の組み合わせになりますので、回転角を間違えないことが大切です。
たとえば、上図の①の回転では、まず中心がRなので、QRが半径となることを確認し、おうぎ形の弧でQからQを結びます。
回転角は、回転前のQRと回転後のQRがつくる角なので、180－60＝120°を書き入れます。
②③④同様に「回転の中心と半径を確認→回転角の書き入れ」を行います。
上図が完成すれば作図はカンペキです。
あとは頂点Qが動いたあとの線の長さ、つまり、半径6cmのおうぎ形の弧の長さの合計を求めます。
120＋180＋60＋180＝540°･･･中心角の合計
6×2×3.14×540÷360＝56.52(cm)

作図の問題は、算数が得意な生徒が意外とミスすることが多いです。
頭の中での処理に慣れているため、細かい書き込みを省略して作図してしまうからです。
確かに頂点記号や回転角の書き込みは大変ですが、「省力せず書き込みを徹底する」ことで驚くほどミスは減ります。
今回紹介したポイントは、正三角形だけでなく「多角形の転がり移動」に共通するものになります。
他の色々な問題で試してみると、より深く身につくと思いますので、ぜひ参考にしてみてください。

それでは、失礼いたします。