こんにちは。
受験Dr.算数科講師の千葉　誠と申します。

算数を教えていると生徒から「習った解き方と違う」と言われることが多々あります。
算数の問題には解法が複数あることが珍しくありません。
基本的には「自分が一番やりやすい解き方を使う」で問題ないのですが、「複数の解法が使えるようになったうえで」という前提があります。
1つのパターンの問題に対して1つの解法でしか対応できない状態だと、問題を少しひねられただけでつまずいてしまい応用力が身につきません。
理解を深め応用力をつけるためには、1つの問題に対し複数の解法で解いてみることで、多角的な視点を獲得し、それぞれの解法の特徴を理解したうえで最適な解法を選び取ることが重要です。

今回は例として「食塩水と比」の典型的な問題に対し4つの解法を紹介しますので、自身の解法と比較してみてください。

問題

5%の食塩水と19%の食塩水を4：3の割合で混ぜてできる食塩水の濃さは何%ですか。

解説

解法①「面積図」

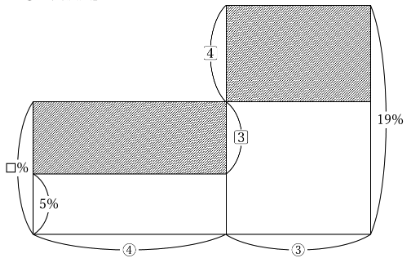
「食塩水と比」を習うときにはじめに教わる解法で、「食塩水の質量×濃さ＝食塩の質量」の関係が視覚的にあらわされていて理解しやすいというメリットがあり、はじめに習う解法としては最適かと思います。
4：3の割合で混ぜるので、5%の食塩水の質量を④、19%の食塩水の質量を③とします。
長方形のよこを食塩水の質量、たてを濃さ、面積を塩の質量、混ぜたあとの濃さを☐%として表すと、かげをつけた２つの長方形の面積が等しくなります。
面積の等しい2つの長方形のよこの長さの比が4：3なので、たての長さの比は逆比の3：4となり、たての長さをそれぞれ、とすると、
＋＝＝19－5＝14(%)
＝2(%)
＝6(%)
☐＝5＋6＝11(%)

解法②「てんびん図」

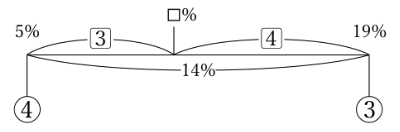
内容は「面積図」同じです。てんびんの両端は混ぜ合わせる食塩水の濃さ、おもりはそれぞれの食塩水の質量、支点は混ぜたあとの食塩水の濃さをあらわします。
「面積図」において面積が等しくなる部分が「つり合いの関係」（支点からの距離×おもりの質量が等しくなる）におきかえられています。
「面積図」よりも図がシンプルで書くのが楽というメリットがあります。
計算は「面積図」と同様なので省略します。

解法③「勝手に決める」
問題設定から、混ぜ合わせる割合が4：3であれば、実際に何グラムであっても答えは1つに決まることがわかるので、それぞれの食塩水の質量を勝手に決めてしまおうという解法です。
濃さは%（百分率）を使うので、勝手に質量を決めるのであれば100の倍数にするのが最適です。
5%の食塩水を400g、19%の食塩水を300g混ぜ合わせると決めると、
400×0.05＋300×0.19＝20＋57＝77(g)・・・できた食塩水に溶けている食塩の質量
77÷(400＋300)＝0.11→11(%)
解法①②で使った「逆比の関係」を理解していなくても解けて、3つ以上の食塩水の混合にも使えるというメリットがあります。

解法④「平均」
これは「勝手に決める」の計算を簡略化したものです。
5%と19%では同じ量の食塩水に含まれる食塩の量は5：19になります。
4：3の質量比の1あたりに含まれる食塩の量をそれぞれ5、19と考えて、混ぜ合わせたあとの食塩水の1あたりに含まれる食塩を計算すると
(5×4＋19×3)÷(4＋3)＝11(%)
これは「5点が4人と19点が3人の平均点」を計算するときと同じですね。
「割合と比」ついてよく理解していないと仕組を納得するのが難しい解法ですが、解法③と同様に3つ以上の食塩水の混合に使えて、計算がより楽になるというメリットがあります。

以上4つの解法を紹介しました。普段自分が使っている解法と比較して、より良いと思うものがあれば取り入れてみてください。

普段学習でも、テキストに別解が載っていた、先生から知らない解法を教わった、解説が自身の解き方と違った、ということがあるかと思います。
その際は自身の解き方に固執するのではなく、貴重な機会ととらえて類題を別解で解いてみるなどして積極的に取り入れていきましょう

それでは失礼します。