みなさん、こんにちは。
受験ドクター算数科の江田です。

心地よい気候が続いていますね。
（暑がりな私にとっては、少し暑いと感じる季節ですが…。）

そして、学校も新学年がスタートしました！
時間割が変わったり
担任の先生が変わったり…
いろいろな変化があることと思いますが、
気持ち新たに頑張っていきましょう！^^

さて、
今日のブログの話題は
「展開図の組み立て」
です。

数日前、
ある6年生の授業で、
そのお子さんが立方体の展開図を頭の中で組み立てようと
必死に考えていた様子を見て、
ぜひこの機会に皆様のお子さんにもチェックしていただければ
と思い、今回のブログでご紹介させていただくことにしました。

では、さっそく…

次のような問題です。
4年生以上のお子さんはぜひご一緒に！
また、低学年のお子さんでも十分正解にたどり着くことは可能ですので、
ぜひチャレンジさせてみてください♪

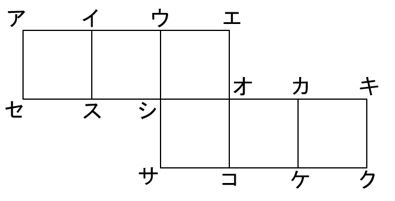
【問題】
下の図は、ある立方体の展開図を表しています。
この展開図を組み立てたとき、図の頂点アと重なるのはどの頂点ですか。
記号で答えなさい。（目標時間は5秒です。）

ご、ごびょう！？

と思われた方も多くいらっしゃったことでしょう。

この問題を
「実際に組み立てた様子を頭の中でイメージする（あるいは図をかいてみる）」
という考えが真っ先に頭に浮かんだ方（お子さん）は、
残念ながら損をしています♪

実は“ある1つのポイントだけ”身につけておくことができれば、
この問題はほんの数秒で解けてしまうんです。
もしかすると、2，3秒かも知れません^^

では、しっかりと確認してくださいね♪

抑えておきたいポイントはこちら！

『立方体の“最も遠い2点”は、展開図上では長方形の対角線の位置にくる』
ということです。

どういうこと？

と思われる方に簡単にご説明いたします。

たとえば以下のような立方体の見取り図を考えてみます。

この立方体の頂点は8個ありますね。
その中で頂点Ａに注目してみましょう。
この頂点Ａから“最も遠い点”は
以下の図の頂点Ｂですね。

（赤い点線は、立方体の中を通る直線です。）

この立方体の上の面を手前に広げた図（展開図）が
下のようになります。

このように、
『立方体の“最も遠い2点”は、展開図上では長方形の対角線の位置にくる』
という性質があるんです。

このことをきちんとおさえたうえで、先ほどの問題を見てみましょう！

この問題は、
頂点アと重なる点を知りたいので、まず
『頂点アから最も遠い点』がどこにいるのか
を考えます。

すると、
以下の図のように“長方形の対角線の位置”にある頂点シとわかります。

ここで、さらに続けて
『頂点シから最も遠い点』がどこにいるのか
を考えます。

すると、
以下の図のように頂点ケであることがわかりますね。

ということで、
頂点アから最も遠い点が頂点シ
頂点シから最も遠い点が頂点ケ
とわかりました。

ん？？

そう！
気付いた方もいらっしゃいますよね♪

頂点アと頂点ケはどちらも
『頂点シから最も遠い点』
ですから、全く同じ頂点です！！

つまり、この展開図を組み立てたときに
まさに“重なる点”とわかるわけです♪

よって答えは
頂点ケ
でした。

いかがでしたか。

中学受験で問われる問題は
“想像力”や“ひらめき”に頼るものも一部ありますが、
今回のように
きちんと性質（根本原理）を理解し、
それをうまく活用することですんなり解くことができる
ような問題も多くあります。

こういったポイントをきちんと身につけながら
着実に力をつけていけるといいですね！

それではまた次回お会いしましょう♪