みなさん、こんにちは。
受験ドクター算数科の江田です。
今回のブログでは
いろいろな小数を分数に直す
ことを一緒に考えてみましょう!
まずは試しに
「中学受験をするならパッと答えられるようにしておきたい数値」
を確認♪
〈問1〉
(1)0.75を分数に直しなさい。
(2)0.625を分数に直しなさい。
さあどうぞ♪
はい!そこまで!
答え合わせです。
(1)は

(2)は

先ほど述べましたように、
この2つは必ずパッと答えられるように
暗記しておくべきでしょう♪
では次の問題です。
〈問2〉
(1)0.342342342342・・・・・(無限に続く)
を分数に直しなさい。
(2)0.6545454545454・・・・・(無限に続く)
を分数に直しなさい。
さあどうぞ♪
…
……
………
…………
はい?

そりゃわからんって(-_-)
そう!
今回メインで触れたいのはこの手のタイプなんです。
見てのとおり、(1)(2)どちらも
ある位から同じ数がくり返される、しかも無限に続く小数
ですね。
このような小数を
「循環少数」
と呼びます。
今回は
「循環小数を分数で表す」
方法を考えてみましょう♪
まず、これらの問題を解く前に
是非みなさん(特に6年生のみんな)に
暗記しておいてほしいことがあります。
それは

以下、同じように考えられる
ということです!
入試問題にもこの手の問題が出題されますが、
親切な学校ですと
問題文の“但し書き”でこのことを教えてくれます。
ただ、特に何も書いてくれない学校も多くありますので
基本的には暗記しておくべき数値と言ってよいでしょう。
さて、
では先ほどの〈問2〉の(1)を見てみましょうか。
0.342342342342・・・・・(無限に続く)
でしたね。
もうお気づきになる方もいらっしゃるのでは?
「342」という3けたの数列がくり返されていますね。
ということは、暗記しておくべきものの1つである

を利用してあげればよいのです。
これを342倍したものがまさに
0.342342342342・・・・・(無限に続く)
となりますね!!
そう、よって分数に直すと

となります♪
いかがですか?
気付けると意外と楽しい!
と思ってほしい(^^;
では〈問2〉の(2)はどうでしょう。
0.6545454545454・・・・・(無限に続く)
でしたね。
うーん、ちょっと難しいですね。
まず
「くり返されている数列」
はどこですか?
そう、今回は
「54」
の2けただけなんです。
ということで、
利用するのは暗記しておくべきもののうちの

なんです。
でも少し引っかかることでしょう。
0.6545454545454・・・・・(無限に続く)
の
はじめの「6」が余計じゃない?
と思いませんか?
そう思った方は、答えまであと一息♪
“余計”ならそれを別にして考えればいいんです。
0.6545454545454・・・・・=0.6+0.0545454545454・・・・・
という感じに。
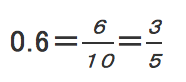
で、
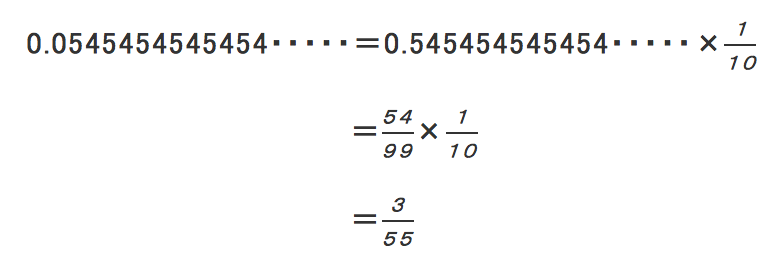
となりますから、
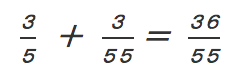
という分数だとわかります。
ちなみに、
この問題の考え方は他にもあります。
たとえば
0.6545454545454・・・・・=0.2+0.454545454545・・・・・
と考えることもできるんです。
そうすると、


となり、

と求められます。
どのように分けられるのか、
人によって考え方は違ってくるかも知れません♪
いかがですか?
面白いと感じた方は
家でも適当に自分で循環小数を作ってみて、
お子様に分数に直させてみてください♪
答え合わせは計算機で確かめてみればよいので、
どなたでも問題を作れると思いますよ。
そして、子どもたちは
自分で求めた答えを計算機に入力してみて合っていたとき、
ちょっとうれしい気持ちになるはず!
是非試してみてください♪
今日はここまで。
また次回お会いしましょう!




