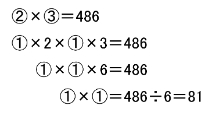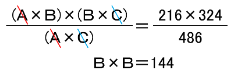みなさん、こんにちは。
受験Dr.算数科の江田です。

今回は中学入試において必須の「比」について理解を深めましょう。
6年生のお子様をお持ちの方は、是非お子様と一緒にご覧になってください。

算数の世界では「比」を使って計算を進めていく場面が多々ありますね。

たとえば
「太郎君と次郎君の速さの比が3：5で、太郎君が学校を出発してから6分後に次郎君が学校を出発し太郎君を追いかけると、次郎君が出発してから何分で追いつきますか」
という旅人算の問題に対して

太郎君の速さを毎分3，次郎君の速さを毎分5として
3×6＝18　　　　　　　……次郎君が出発したときの2人の間のきょり
18÷(5－3)＝9 (分) ……次郎君が出発してから追いつくまでの時間
といった考え方ができます。

この場合、「比を実際の数値(実際の速さ)」として計算しているわけです。
もちろん、これは実際の速さではなく「比」の数値なので、
本来は毎分③や毎分⑤というように◯などの記号で囲って使っていくべきものです。

平面図形の問題で、長さの比が与えられたときに◯や□、あるいは△などで囲った数値を図の中にかきこみますよね。それと同じことです。
「実際の数値」ではなく、あくまでも「比」なのでそれを区別するために記号をつけているのです。

これを使って、先ほどの旅人算は
③×6＝⑱
⑱÷(⑤－③)＝⑱÷②＝9 (分)
と求めていることになります。

では次の問題はどのように解いていけばよいのでしょう。

【問】
3つの整数Ａ，Ｂ，Ｃがあり、
Ａ×Ｂ＝216
Ｂ×Ｃ＝324
Ａ×Ｃ＝486
のとき、Ａ，Ｂ，Ｃをそれぞれ求めなさい。

この問題の解法はいくつかあるのですが、今回は「比」の理解をテーマにしているので「比」に注目した解法を見ていきます。

まず、与えられた3つの式をそれぞれ
Ａ×Ｂ＝216　……㋐
Ｂ×Ｃ＝324　……㋑
Ａ×Ｃ＝486　……㋒
とします。

たとえば㋐と㋑の比をとると

であることがわかりますね。

A＝②，C＝③とし、㋒の式に代入すると
②×③＝486
となるので、
486÷(2×3)＝81
という計算式を思い浮かべた方も多いのではないでしょうか。

さて、この式で求めた81は一体何のことでしょう。
①の値としては大きすぎるような気がしますよね。
もし①＝81だったら
A＝81×2＝162
C＝81×3＝243
となり、
A×Ｃ＝162×243＝39366
になってしまいます。

何がいけないのでしょうか。

気付きましたか？

この「②×③」が⑥ではないのです！

「②×3」であれば「②が(実際に)3個ある」ので⑥になりますが、
「②×③」は「②が(比の数値で)③個ある」という意味なので、
この値が絶対に⑥になるとは言い切れないのです。
(①＝1だった場合のみ、「②×③＝⑥」が成り立ちます。)

比の数値と比の数値をかけた積が何を意味しているのか。
その正しい理解が必要となります。

先ほどの【問】において
②×③＝486
とありましたね。
この②と③はそれぞれ、「ある同じもの(数値)」をもとにしたときにその2倍であること、その3倍であることを表したものです。

つまり、その「ある同じもの(数値)」を①とすれば
②＝①×2
③＝①×3
と表すことができ、

となります。
そう、この81は①×①の値だったんですね。

よって、①＝9とわかり
A＝9×2＝18
C＝9×3＝27
と求まります。
残りのBは㋐の式から
216÷18＝12
と求められます。

ちなみに今回紹介した【問】は
Ａ×Ｂ＝216　……㋐
Ｂ×Ｃ＝324　……㋑
Ａ×Ｃ＝486　……㋒
の3つのうち、「どれか2つをかけて、残った1つで割る」というやり方もできます。
たとえば「㋐と㋑をかけて㋒で割る」と、

というように、Bの平方数がわかるので
B＝12
と求められます。

いかがでしょう。
おそらく、今回の問題を解くうえでは
このやり方のほうがわかりやすい受験生も多いかと思います。

ただ、比の意味・使い方をしっかりと理解しなければ、問題を解き進めるなかで混乱が生じやすい問題も難関校には多く出題されています。

次回はそんな問題を扱いますのでお楽しみに！