みなさん、こんにちは。
受験Dr.算数科の江田です。

今回は、中学受験算数において必ず頭に入れておきたい図形についてのお話。

それは「30゜，60゜，90゜の直角三角形」です。

いろいろな場面で見かけるこの図形。
みなさん（のお子様）は正しく理解・定着できていますか？

というのも、
「30゜，60゜，90゜の直角三角形」と「3：4：5の直角三角形」を混同している
生徒がちらほら見受けられるので、これを機にはっきりさせておこうと思いまして…。

もちろん、
これらの直角三角形を2つならべて目の前に出されれば
「同じものじゃない」と判断できる生徒も多いかと思いますが、
図の中に潜んでいるこれらの図形を見つけた際に、
区別できずにごちゃ混ぜになってしまうケースが少なくないのです。

 

まずは下の図のような「30゜，60゜，90゜の直角三角形」について。
知っている方も多いでしょう。

 

 

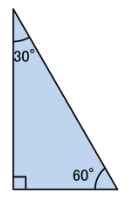
そう、三角定規の片方がこのかたち。
この直角三角形2枚を次のようにつなげれば正三角形ができるので、
3辺のうち最も長い辺（斜辺）と最も短い辺の長さの比が2：1とわかりますね。

 

 

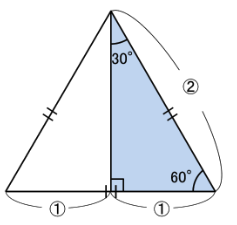
この「30゜，60゜，90゜の直角三角形」は中学受験算数においては
メチャクチャ大事！！
常に頭の片隅に置いておくようにしましょう！

次に「3：4：5の直角三角形」について。
下のようなかたちですね。

 

 

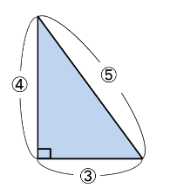
もちろん、これを2枚つなげても正三角形にはなりません。
先ほどの「30゜，60゜，90゜の直角三角形」とは全くの別モノです。

ただ、たしかにこの直角三角形もよく目にします。
だからこそ、混同してしまう受験生が少なくないのでしょう。

中学生になれば
「ピタゴラスの定理(三平方の定理)」を学習するので
区別しやすくなるかも知れません。

ちなみに「ピタゴラスの定理(三平方の定理)」とは
直角三角形において
斜辺(最も長い辺)の長さをＡ，それ以外の2辺の長さをＢ，Ｃとしたときに
Ａ×Ａ＝Ｂ×Ｂ＋Ｃ×Ｃ
が必ず成り立つというもの。

たとえば3辺が3㎝，4㎝，5㎝の場合は
5×5＝3×3＋4×4
で成り立っていますね。

この等式を満たす
3つの「整数の」組み合わせとして最もシンプルなのが3と4と5
というだけであって、他にも
5と12と13
7と24と25
8と15と17
9と40と41
などなど…
いくらでもあります。

それらのうち、
中学受験において出題される図形に使われる最も代表的な組み合わせが
「3：4：5」
だというだけのお話。
次に多く目にするのは
「5：12：13」
かな…といった感じです。

もちろん他の組み合わせになっていることもありますし、
そもそも3辺の長さがすべてわかる必要がない(あるいは整数の組み合わせである必要がない)問題も多くあり、

 

 

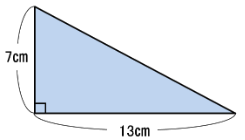
のような直角三角形が出題されている可能性もあるわけです。
※この場合は斜辺の長さは(小学生のうちは)求められません。

ですので、暗記するのであれば
「3：4：5」とか「5：12：13」などの組み合わせは
以上のことをきちんと理解したうえで暗記しましょう！

ちなみにこれらの組み合わせを覚えていないと答えが求まらないような問題は
“基本的には出題されない”と思ってよいでしょう。
もし、この組み合わせを利用しなければ解けないような問題が出題されるとするならば
問題文のなかに「必要であれば次の性質を利用しなさい」などの文面があることがほとんどです。

ただ、ごく一部の学校では
この組み合わせを知っていることを前提とした問題が過去に出題されていますので、
6年生の9月以降に取り組むことになるであろう自身の志望校の過去問演習の際に
ちょっと気にしてみてください。

 

ということで結論です。

➀「30゜，60゜，90゜の直角三角形」は超大事！絶対に覚える！
➁「3：4：5の直角三角形」は無理に覚える必要なし！
※覚えるのであれば性質を理解したうえで、区別しておさえましょう。

次回は
立体図形において「頭に入れておくべき図形」に触れたいと思います。

それではまた次回お会いしましょう！