みなさんこんにちは。
理科・算数担当のT.H.です。
前回のブログで、格子状のてこを合成重心で解く方法を扱いました。
今回はその解法だと少し戸惑ってしまうような問題について、対処法を紹介します。
下図のような格子状の枠組みの中心を糸でつり上げました。
ここに10gのおもりを2つ、それぞれ(E、2)と(F、5)の位置につるしました。
10gのおもりをもう1つどこかにつるして、枠組み全体がつり合うようにします。
どの位置につるせば良いか答えなさい。
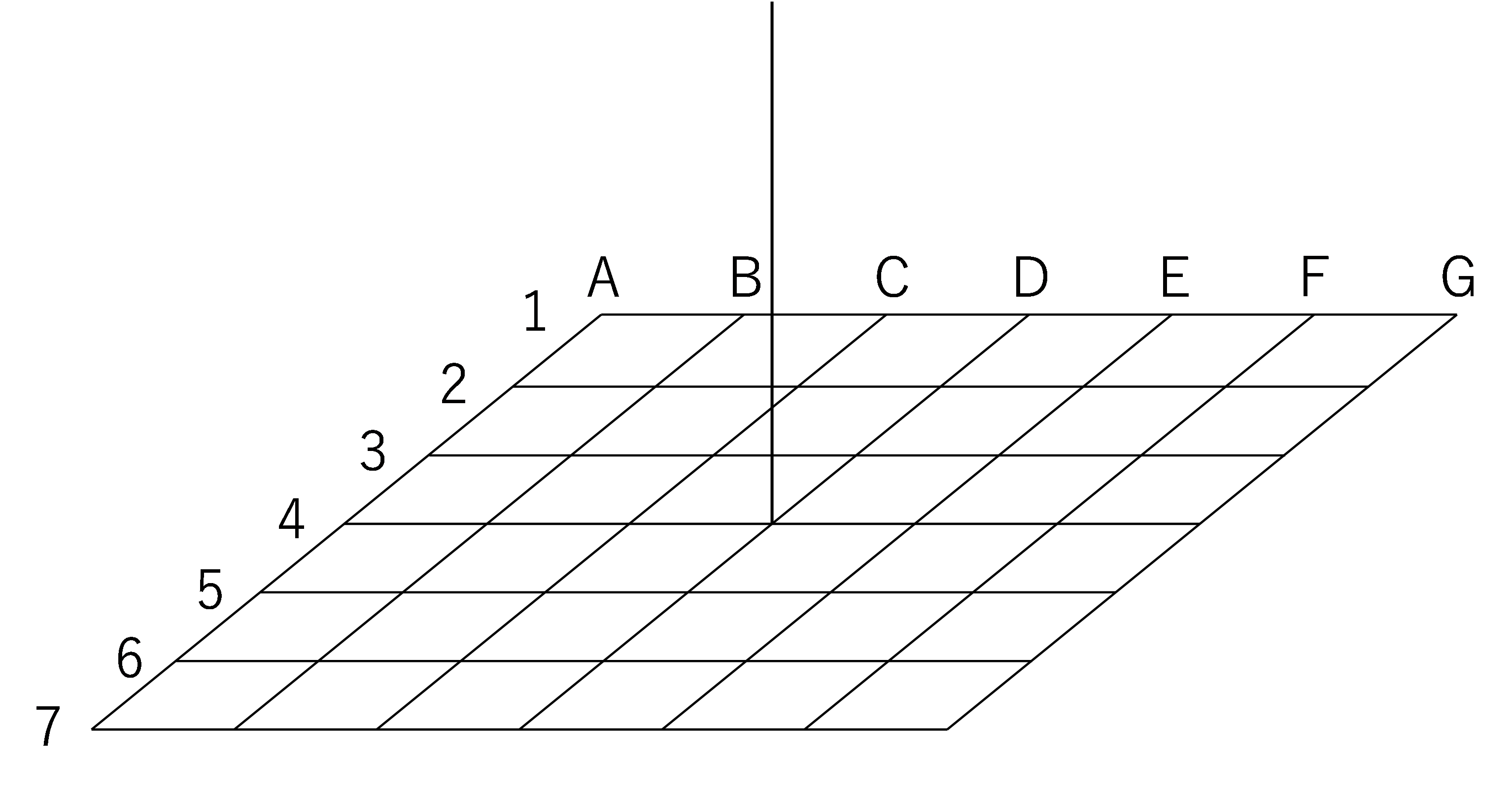
前回同様に合成重心の位置を考えると、下図のような中途半端な位置になってしまいます。
このままでも解くことはできますが、計算に分数や小数が含まれるとどうしてもミスしやすくなります。
計算や考え方の複雑化はできる限り避けたいので、整数のみで計算できる方法があるとベストです。

そこで今回紹介する2つ目の考え方が 「2方向から見るつり合い」 です。
この装置がつり合っているのであれば、前後左右どの方向から見てもつり合って見えるはずです。
まず前(正面)から見た図でつり合いを考えます。

前から見た場合は奥行きを無視できるので、下図のような平面のてこのように見えます。

ひもでつり上げている部分を支点とすると、
右側のおもり2つのモーメントは 10g×2マス+10g×1マス=30
10gのおもりでつり合わせるには、支点からのキョリが 30÷10g=3マス、Aにつるす必要があります。
上から見た図だと、おもりをつるす位置は下図の赤枠の範囲とわかります。

同様に右(横)から見た図でつり合いを計算します。


右上図において、時計回りのモーメントは 10g×2マス=20
反時計回りのモーメントは 10g×1マス=10
これをつり合わせるには20-10=10の反時計回りのモーメントが必要になるので、
10÷10g=1マス 、したがって5の位置ということが分かります。
さきほどの上から見た図に書き加えると、

前から見た位置と右から見た位置の重なる場所、(A、5)が答えであるとわかります。
このように、2方向から見てつり合わせると、すべて整数だけで計算することができました。
前回の「合成重心」と、今回の「2方向のつり合い」は、どちらも一長一短で、どちらも有用です。
・合成重心 ⇒ 計算手順が少なく、早く計算できる。
・2方向のつり合い ⇒ 計算途中に分数や小数が出てこない。
まずは1種類の解き方を極めることも大切です。
しかし手順に詰まったとき、別の切り口から考えられると、対応できる問題の幅が広がりますし、
適切な解法を選ぶことで時間短縮にもなります。
(2種類の解法を両方使うことで答えの見直しにも便利です。)
授業や参考書などで自分の知らない解き方を習ったら積極的に身につけて、
様々な入試問題に効率よく取り組みましょう。




