こんにちは。受験ドクターのI.Sです。

中学受験の算数には、「解き方を知らないと非常に厳しい」という問題がいくつかあります。
基本知識の組み合わせではなく、ある程度飛躍した考え方が求められる問題です。
今回はそのうちの一つである、時計算の問題をご紹介します。
5年生・6年生共通で多くの受験生が悩む問題です。

「3時から4時の間で、長針と短針のつくる角が、文字盤の5を通る直線によって2等分される時刻は3時何分でしょうか」

このような問題です。
この問題は、ある解き方を知っていると、非常に簡単に考えることが出来ます。
とても面白い考え方なので、是非ご覧ください。

まず手順を先に説明し、その後で理屈を解説します。

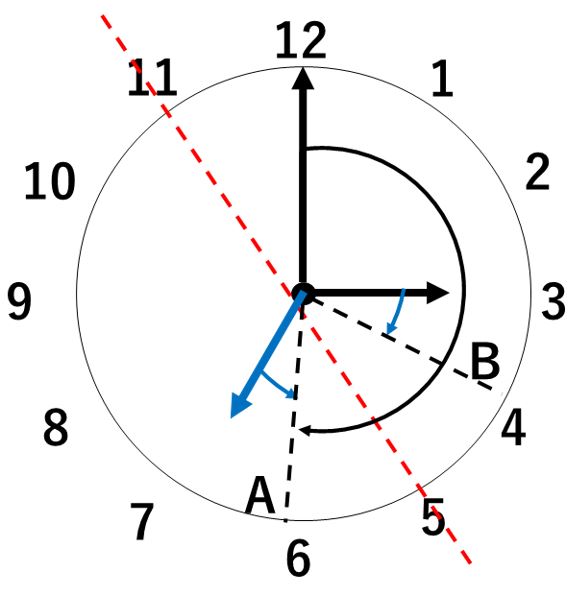
① まず3時ちょうどの絵を描き、対称軸となる5時の位置に線を引きます。

② 対称軸となる5時の線から、鏡合わせの位置（線対称の位置）に、「ニセモノの短針」を作ります。
図の青い短針が「ニセ短針」です。
本物の短針は3時の位置にあるので、対称軸である5時の線からは2メモリ離れています。よって、ニセの短針は7時の位置になります

③ このニセ短針は、逆向き（反時計回り）に動きます。ニセ短針と長針が出会う（重なる）時刻を計算します。

【計算】
長針とニセ短針の間の角度は　30×7＝210°です。長針は1分間に6°動き、ニセ短針は1分間に0.5°動きます。よって
210÷（6+0.5）＝
となり、 分が答えとなります。
下の図のように、Aの時刻に、ニセ短針と長針が出会います。

④ この時刻が、問題の答えです。　　　　　答え：

以上です！簡単ですよね。
では、どうしてこの考え方が成り立つのか、理屈の部分を説明していきます。

ニセ短針がAの位置まで動いたときに、本物の短針はどこにいるか？　を考えます。
ニセ短針がAの位置に行くまでに動いた角度と同じ角度だけ、本物の短針も動いています。
ですから、本物の短針は、図のBの位置にいることになります。
このときの長針は、もちろんAの位置にあります。
すると、AとBは赤い線（5時の線）を挟んで対称の位置になっていることが分かります。

このように、「文字盤の〇を通る直線によって2等分される時刻」という問題は「文字盤の〇の直線から鏡合わせの位置にニセの短針を作り、逆向きに動くニセ短針と長針の出会う時刻を計算する」という問題に置き換えることが出来ます。

これは知らないとなかなか思いつかない発想です。
中学受験の算数は、考えればその場で解法を思いつくことの出来る問題もありますが、このような問題は解き方を知っているかどうかで大きく差がつきます。
問題の本質を小学生が理解しやすい形に整えて、覚えやすい形で知識をインプットしてあげたいです。
（そのために「ニセ短針」のようなキャッチ―な造語を使うような工夫もします）

解法の暗記はなるべく避けたいですが、どうしても避けて通れない部分があります。せっかく覚えるなら、出来るだけ覚えやすい形で学習させてあげたいと思います。