こんにちは。受験ドクターのI.Sです。

今回は、補助線の引き方講座をやっていきます。

平面図形でよく耳にする「補助線をどこに引いたら分からない！」という悩みを解決していきます。
決してセンスに頼らない、誰でも引けるようになる方法がありますので、お伝えします。
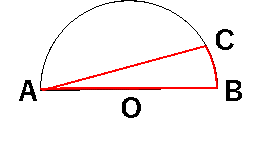
今回のテーマは「曲線を含んだ変な形」です。例えばこんな形です。

問題：半径が4㎝の半円上に、角CAOが15°となるように、円周上に点Cを取りました。赤い線で囲まれる部分の面積は何㎠でしょうか。

このような問題で、どこに補助線を引けばよいのか？　実は、明確な方法があります。

その前にひとつ、中学受験算数の前提をお話します。
それは曲がった線（カーブ）は、全て円の一部（弧）だ！と言うことです。
中学受験の範囲ではまだ放物線や楕円といった、円以外の種類の曲線は登場しません。
つまり、出題された図で線が曲がっていたら、それは円の一部（弧）だと判断して良いということです。

そんなの、当たり前でしょうか？　いえいえ。これを利用すると、とても便利なことがあります。

「カーブを含んだ変な形」の面積を求めるなら
カーブの両端と、円の中心を補助線で結ぶ
です！　これが、ほとんどの場合に当てはまる補助線の引き方です。
先ほどの例で見てみましょう。

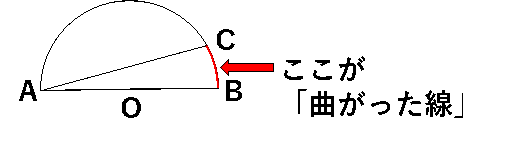
上の図の赤で示された部分が「曲がった線」です。
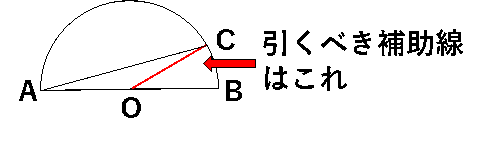
この曲がった線の「両端」とは、点Cと点Bですね。円の中心は点Oですので、点Cと点Oを結ぶ線
が今回引くべき補助線ということになります。
実際に引いてみると、下図のようになります。

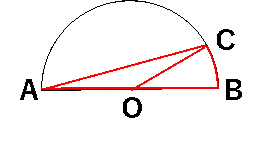
すると、下図のように、扇形OBC（中心角30°）と、三角形OCA（150°-15°-15°の二等辺三角形）の二つに分割することが出来ます。

扇形と三角形の面積をそれぞれ別々に求めて、足し合わせれば答えを出すことが出来ます。
（150°-15°-15°の二等辺三角形の性質については、別の機会に持ち越します）

図形が複雑になったとしても、初見の図形だとしても、「曲がった線を含む変な形」の面積を求める場合は、ほとんどの場合この法則が当てはまります。
曲がった線の両端と円の中心を結ぶ補助線を引いて考えることが第一歩です。

もう一問例題を出してみましょう

問題：下の図のように、半径３㎝の半円があります。
弧BCを3等分する点を、E，Dとします。
赤い斜線部分の面積は何㎠でしょうか。

さて、この問題も、分野としては「曲線を含んだ変な形」に該当します。
先ほどの法則通りに曲線の両端と円の中心を結んでみます。
すると下の図のようになります。

まずはこの2本の線（OEとOD）を作図してから考えます。
すると、赤い斜線部分の面積は
扇形EOD＋三角形EFO－三角形OGD

で求められることが分かります。
三角形EFOと三角形OGDは合同ですから、答えは扇形EODの面積を求めればよいということが分かります。

このように、まずは曲線の両端と中心を結ぶ線を引いてみることが大切です。

補助線が引けるかどうかは、決してセンスの有無ではありません。
きちんとした引く際の基準、引き方を習得しているかが大切なのであり、練習次第で誰でも出来るようになります。
センスや才能に頼らない解法の指導を心がけております。

それではまた！