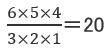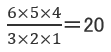A,B,C,D,E,Fの6人を、3人ずつの2グループに分けます。分け方は何通りですか。ただし……

問題1：2つのグループには「桜組」と「椿組」という名前が付いています。
問題2：2つのグループには特に名前はついていません

 

こんにちは。受験ドクターのI.Sです。
突然ですが問題を二問出してみました。

上の二問の答えは、同じになるでしょうか。それとも別の答えになるでしょうか？

 

正解は、別の答えになる、です。
①の答えは20通りで、②の答えは10通りです。
「ええ？同じ問題じゃないの？」
という疑問を解消すべく、今回はこの問題について解説していきます。

 

まずは①から行きましょう。

6人の中から、まずは桜組に誰を入れるかが何通りあるのかを計算します。
これはか6人から3人を選ぶ組み合わせですので

 

 

となり、20通りが答えです。
（6C3 のようにコンビネーションを使って考えてもOKです）

 

ここまでは場合の数がある程度分かっている子ならば「当然でしょ～」という顔をしているはずです。

 

では②に移りましょう。

さて、①と②で何が異なっているかというと、グループに名前が付いているかいないかです。

言い換えると、２つのグループが区別できるかどうかが異なっています。

具体例を出してみましょう。

 

問題①で、例えば　「桜組：A,B,C 椿組：D,E,F」の場合と「桜組：D,E,F　椿組：A,B,C」は別のものとして数えます。
しかし問題②で「A,B,CとD,E,F」のグループに分けた場合と「D,E,FとA,B,C」のグループに分けた場合に、違いはあるでしょうか？　グループ名がついていない場合、この2通りは同じものになってしまいます。

 

そのため、ダブりを消すためには、①で求めた20通りからさらに÷2する必要があります。つまり

 

 

より答えは10通りになります。

場合の数の問題では、区別できるかできないか。という点がとても重要になってきます。

問題文で「3つの箱があり、赤・青・緑に色分けされています」のような文章が良くあります。これはつまり「この3つの箱は区別できるものとして計算しますよ」という合図なのです。箱の区別がつく場合とつかない場合では答えが変わってきます。

人を部屋に振り分けるような場合では、部屋に名前が付けることで「区別するものだ」ということを受験生に伝えようとしています。
他に見たことがある表現では「2つの部屋があり、片方の部屋は角部屋です」であったり「片方の部屋は和室で、もう片方の部屋は洋室です」のようなものも見たことがあります。

この点を意識していない生徒にとっては「なんだか無意味なことが書かれているなぁ。角部屋かどうかなんて算数に関係あるの？」と思ってしまうかもしれません。
でもこのブログを読んでくれた方ならば「これはつまり区別するってことなんだな」と気づけます。

 

知っているだけでちょっと得する情報。ぜひお子様にも教えてあげてください。

受験ドクター算数科の石井伸二でした。