みなさん、こんにちは。受験ドクターの亀井章三です。
3月になり暖かい日も多くなってきましたね。天気の良い日は日当たりの
良い公園を散歩して、気分をリフレッシュするのもいいですね。
今日は受験算数でも頻出の「平面図形と面積比」についてです。
三角形をいくつかの直線で分割し、辺の比や面積比を考える問題です。
実際に問題を見てみましょう。
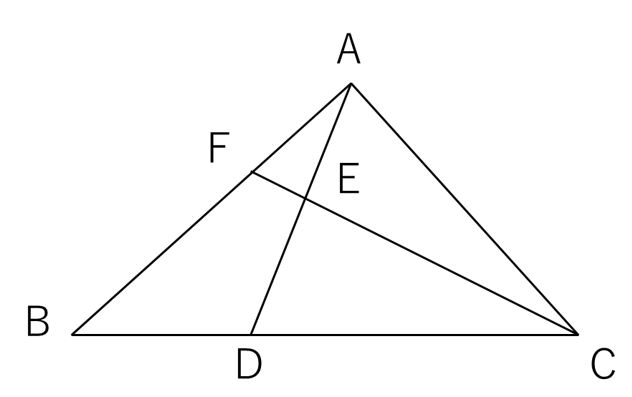
辺BCの上に、CDの長さが8㎝となるように点Dをとります。また、ADの上にAD:AEが5:2となるように点Eをとり、CEをEの方に延長したものと辺ABが交わる点をFとします。このとき、次の問いに答えなさい。
(1)ABとAFの長さの比をもっともかんたんな整数の比で答えなさい。
(2)三角形ACFの面積は三角形AEFの面積の何倍ですか。
【大阪桐蔭中 2016年・改題】
この問題はいろいろな解き方が考えられます。
①補助線を書いて相似形を作る
②メネラウスの定理を使って解く
③補助線BEを引いて面積比を利用して解く
今回説明するのは、③の考え方を「視覚的にわかりやすく」解く方法です。
それが「てんびん」です。
理科でも出てくるてんびんには2つの決まりがあります。
<1>支点からの距離と重さの積が支点の左右で等しくなる
⇒重さの比は支点からの距離の逆比になる
<2>左右の重さの合計と支点にかかる重さは等しくなる
このことに留意して問題を解いてみましょう。
まずは、比がわかっている部分に比を書き込みます。
BD:DC=4:8=1:2 AE:ED=2:(5-2)=2:3
次に、比がわかっている直線を「真ん中が支点であるてんびん」に置き換えます。
まずは辺BCで考えましょう。
イメージしやすいようにてんびんの両端B、Cのところにおもりをぶらさげてみました。
では、このてんびんを釣り合わせるためには、BとCにぶらさげるおもりの重さは
どのような比にすればよいでしょう?
それは、支点からの距離の逆比でしたよね。BD:DC=1:2なので、
B:C=2:1となります。
そして、そのとき支点Dにかかる重さの比は1+2=3と表すこともできます。
今度はADのてんびんを同じように考えてみましょう。
Eを支点として、AE:ED=2:3なので、AとDにぶらさげるおもりの重さの比は、
A:D=3:2となります。そして、支点Eには5の重さがかかります。
すると、点Dには2種類の重さが書かれています。これを最小公倍数にそろえ、
2つの比を連比でそろえます。
これで問題を解く準備は完了です。
(1)ABとAFの長さの比をもっともかんたんな整数の比で答えなさい。
ABとAFの比なので辺ABに注目します。
すると、Aに9の重さのおもり、Bに4の重さのおもりがぶらさがっていることがわかり
ますね。これでABのてんびんはつりあっていますので、AF:FB=4:9とわかります。
したがって、AB:AF=13:4 と求められます。
(2)三角形ACFの面積は三角形AEFの面積の何倍ですか。
これは、CFとFEの比を求めることで答えることができます。
そこでCFのてんびんを見てみましょう。
点Fにはまだおもりがぶらさがっていませんので、AとBの重さの合計である
13のおもりをぶらさげます。Eに15のおもりがぶらさがっているので、15-2で
求めても構いません。
すると、F:C=13:2より、FE:EC=2:13、CF:FE=15:2と求められます。
したがって、三角形ACFの面積は、三角形AEFの面積の、15÷2=7.5倍に
なります。
いかがでしたか、三角形で頂点から向かい側の辺に向かって直線が引かれた
このような図形では、てんびんで比を視覚化することでわかりやすく解くことがで
きます。ぜひお子様といっしょにいろんな問題で試してみてください。