みなさん、こんにちは。受験ドクターの亀井章三です。
今回は旅人算で、問題文をどのように図に描いていけば
よいのか、についてお話しさせていただきます。
ポイントは絵描き歌です。
みなさんは、絵描き歌と聞くと何を思い出しますか?
可愛いコックさん、あの有名なネコ型ロボット、
いろいろありますよね。
絵描き歌は、絵の描き方を歌詞にし、歌いながら絵を描いていくことで
最後には絵が完成する、というものです。
この歌いながら描くというのが重要。
と言っても、算数の問題を解く時に毎回声に出し、問題を読みながら
図を描きましょう!というわけではありません。そんなことをしたら
試験会場から追い出されてしまいます。
歌のように、少しずつ描いていくことで、最後には完成する、
これが旅人算の図の描き方にも共通するということです。
実際に問題を使って、描き方を見てみましょう。
たかし君とまこと君が全長6㎞のマラソンコースを同時にスタートし、そ
れぞれ一定の速さで走り始めました。たかし君はスタートして3.6㎞の地点Pか
ら、それまでの半分の速さで走りました。たかし君が地点Pを通り過ぎた15分後
から、まこと君はそれまでの2.5倍の速さで走りました。まこと君はゴールまで残
り600mの地点でたかし君を追い抜いて先にゴールしました。また、たかし君はス
タートしてから40分後にゴールしました。
文章の改行箇所は出題されたものと同じです。
それでは図を描いていきます。
問題文を一文ずつ区切って、そこまでの状況を図にします。
★たかし君とまこと君が全長6㎞のマラソンコースを同時に出発し、それぞれ
一定の速さで走り始めました。
ここで描くべきは、「たかし」「まこと」「6㎞」「同時に出発」です。
下のように描きます。
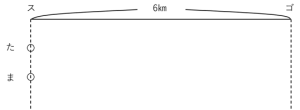
同時を表すには、同じ記号(ここでは○)を使いましょう。
★たかし君はスタートして3.6㎞の地点Pから、それまでの半分の速さで走り
ました。
ここで描くべきは、「3.6㎞」「地点P」「半分の速さ」です。
下のように描きます。
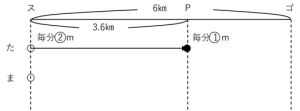
半分の速さは、②と①で表します。
★たかし君が地点Pを通り過ぎた15分後から、まこと君はそれまでの2.5倍
の速さで走りました。
ここで描くべきは、「15分後」「2.5倍の速さ」です。
下のように描きます。
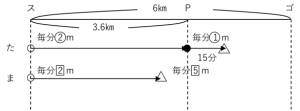
まことの「速さ2.5倍」は、2と5を用いて表します。
★まこと君はゴールまで残り600mの地点でたかし君を追い抜いて先にゴール
しました。
ここで描くべきは、「ゴールまで残り600m」「追い抜いて」「先にゴール」です。
下のように描きます。
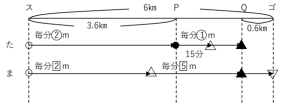
まこと君が追い抜いた場所に名前がないので、地点Qとします。
★また、たかし君はスタートしてから40分後にゴールしました。
ここで描くべきは、「40分後」「たかしがゴール」です。
下のように描きます。
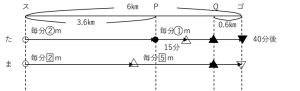
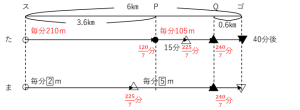
これで図は完成です。
かなり情報が書き込まれていて、わかりやすくなっています。
それでは設問にうつりましょう。
(1)たかし君がスタートしたときの速さは分速何mですか。
たかし君がゴールするまで40分かかりましたので、
かかった時間を式にします。
3600÷②+2400÷①=40
3600/②+2400/①=40
3600/②+4800/②=8400/②=40
8400÷②=40 ⇨ ②=210m/分
図を見ることで何をすべきかが分かりやすくなりました。
次の設問です。
(2)まこと君がスタートしたときの速さは分速何mですか。
まず(1)で求めた数値、そこから計算できる数値を図に描き加えます。
赤字が書き加えた箇所です。
ここから、まことも合計240/7分で5400m進んだことがわかります。
2 ×225/7+5 ×15/7=5400
450/7 + 75/7 = 525/7 = 75 =5400
2 =5400×2/75=144 よって、答えは毎分144mです。
図を描けば、今回のように計算式で解いてもいいですし、比を活用して
解いても構いません。大事なのは、
①問題文の状況を正しく全て図にすること、
②分かったことを図に描き足して図を活用すること
の2点です。この2点をおさえておけば、速さの文章題も怖くありません。
ぜひお試しください。