みなさん、こんにちは。受験Dr.の亀井章三です。
今回は、速さの問題において、時間とともに変化していく「距離の和」を
グラフを用いて捉える方法についてです。
まずは次の問題をご覧ください。
A君の家とB君の家を結ぶ道の途中に学校があります。
A君の家から学校までは2400m、B君の家から学校までは2000mです。
今、A君とB君が学校を同時に出発し、学校と自分の家の間を何度も
往復しながら1時間歩き続けます。
A君の歩く速さは毎分160m、B君の歩く速さは毎分200mです。
A君とB君の間の距離が2400mになるのは、出発してから何分後ですか。
全て求めなさい。
このように、状況(2人の間の距離が2400mになる)を自分で考えないといけない
問題では、細かく図を描いていくのは大変です。
そういう時こそグラフを作りましょう。そうすれば、複雑な状況も簡単に理解すること
ができます。
A君とB君の間の距離ですが、これは「学校とA君の間の距離」と「学校と
B君の間の距離」の和になっています。
そこで、2つの距離の和を、次の手順でグラフにします。
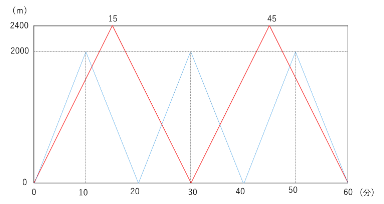
1 それぞれの距離のグラフを、1つの枠の中に描
2400÷160=15 A君は片道進むのに15分、1往復に30分かかります。
2000÷200=10 B君は片道進むのに10分、1往復に20分かかります。
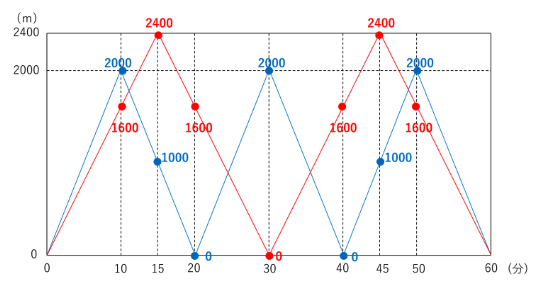
2 グラフが折れ曲がった時の値(距離)をそれぞれ求めて記録する
グラフが折れ曲がっていない直線の部分は、進む方向や長さの増減が変化せず
一定であるため、和の変化も一定になります(グラフが折れ曲がることはない)。
そこで、それぞれのグラフで折れ曲がった時だけ値を求めておきます。
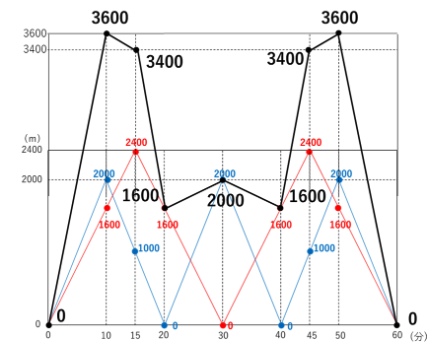
3 ②で記録した値の和を求めグラフ上に打点し、結んでグラフにする
先ほど求めた各グラフの値の和を求め、それをグラフにすると和のグラフが
完成します。
このグラフを使えば、距離が2400mになる時間も求めやすくなります。
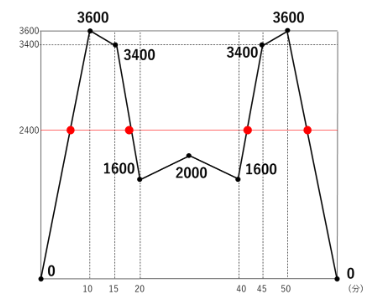
グラフをよく見ると、左右対称になっていることが分かります。
そこで、20分までの最初の2回の時間を求めれば、40分以降の残り2回の
時間も求めることができます。
1回目は10分後までに起こっています。
3600÷10=360 より、この10分間は毎分360mずつ距離が広がっています。
1回目は10分後までに起こっています。
3600÷10=360 より、この10分間は毎分360mずつ距離が広がっています。
よって、2400÷360=![]() 分後と求まります。
分後と求まります。
2回目は15分後から20分後までの間に起こっています。
(3400-1600)÷(20-15)=360 より、この5分間は毎分360mずつ距離が
縮まっています。
よって、(3400-2400)÷360=![]() 分後と求まります。
分後と求まります。
今回のポイント
・グラフが折れ曲がるところだけ調べて和のグラフを作る
・グラフが線対称のときは、対称性を利用し計算する手間を節約する
次回もよろしくお願いします。