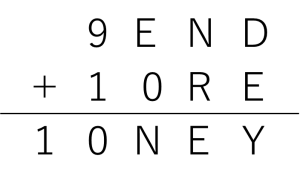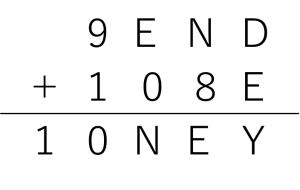みなさん、こんにちは。受験Dr.の亀井章三です。

今回は「ふくめん算」です。ふくめん算というのは、算数の計算（筆算）で数字に
文字のふくめんがつけられているのを、ふくめんを外して元の数字に戻していく
というパズル的要素の強い問題です。
1924年にデュードニーというパズル作家が雑誌に紹介した次の問題が最初の
ふくめん算と言われています。

 

それぞれの文字に入る数字を答えなさい。

 

使われている文字は、S、E、N、D、M、O(オー)、R、Yの８つです。
ふくめん算には大切なルールがいくつかあります。
・同じ文字には同じ数字をあてる
・同じ数字が異なる文字に入ることはない
・どの行でも一番大きな位の文字に0（ゼロ）が入らない

この問題の解き方を通して、ふくめん算攻略のポイントを解説します。

 

１ 数の範囲を用いて数字を決める

この問題では2つの4ケタの数SENDとMOREを足したら、
答えが5ケタの数MONEYになっています。
最も大きい４ケタの数は9999です。
したがって、9999＋9999＝19998となり、M=1と決まります。

そうするとMOREの千の位も１となり、MOREは2000未満の数と分かります。
MONEYが10000以上の数なので、10000－1999＝8001より
SENDは8001以上9999以下の数と分かります。

さらに、1999＋9999＝11998　より　MONEYは12000未満の数と分かります。
Mに1が入るため、Oに1を入れることができません。
よって、O（オー）=0（ゼロ）と決まります。

このようにある数の範囲が決まることで、他の数の範囲も決まっていき、
繰り返すことで徐々に数字が決まっていきます。
さらに続きを見ていきましょう。

 

２ 入る数字の候補が2つある時は、どちらか一方に仮定する

MOREは10□□　という形になるため、1000以上1099以下になります。
ここで、S=８、つまりSENDが9000未満であると仮定します。
9000未満の最大の数は8999、8999＋1099＝10098　より
Nは0しか入らないことになります。既にOが0と決まっているため、これは
ルールに反します。これを「矛盾」といいます。
矛盾があったということは、仮定が間違っていたことになります。
SENDが9000未満であるという仮定が間違っていたので、正しくは
SENDは9000以上の数であることになり、S=9と決まります。

ここまでの状況をまとめます。

 

 

３ 繰り上がりがあるかどうかを考える

百の位だけを見ると、E+0＝Nとなっています。
ルールから、EとNには異なる数が入るはずです。これはどういうことでしょうか。
それは、十の位の計算の結果、繰り上がりが生じたことで、
1＋E＋0＝Nとなっている、というわけです。

NはEより1大きい数になるので、E=3、N=4として十の位を考えます。
N＋R=E　のEに3、Nに4を代入すると、
4＋R=3となります。
先ほど十の位の計算の結果繰り上がりが生じると分かったので、
この式は、4＋R=13となります。
これを計算するとR=9になりますが、既に9はSに入ることが決まっています。
ここでも繰り上がりが関係しています。
つまり、一の位の計算の結果、繰り上がりが生じ、
1＋4＋R＝13　となったと考えることができます。よって、R=8が決まります。

ここまでの状況をまとめます。

 

 

残った文字は、E、N、D、Y
残った数字は、2、3、4、5、6、7
分かっていることは、E+1＝Nになることと、D＋Eの答えが10以上になる
ということです。

 

４ 残りの組み合わせを全て調べ上げる

ここまで来たら最後は全ての組み合わせを調べていき、正解にたどり着きましょう。
Eに入る数の候補は、2、3、4、5、6の5通り

そして、D+Eの答えが10以上になることから、（D、E）の組み合わせは
（7、3）（6、4）（7、4）（6、5）（7、5）（5、6）（7、6）の7通りになります。

YはD+E－10で求められるので、（D、E、Y）の組み合わせを作ると
（7、3、0）（6、4、0）（7、4、1）（6、5、1）（7、5、2）（5、6、1）（7、6、3）となります。

Yに入る数も2～7となりますので、（D、E、Y）＝（7、5、2）と（7、6、3）の2つが
条件を満たします。

最後はE+１＝Nの条件を用いると、E=6のとき、N=D=7となってしまうため、
D=7、E=5、Y=2、N=6　と決まります。

正解は、9567＋1085＝10652　となり、
S=9、E=5、N＝6、D=7、M=1、O=0、R＝8、Y=2　になります。

 

今回のポイント
・ふくめん算では、数字のケタ数に着目し範囲を絞っていく。
・候補が2つある時は片方が正しいと仮定する。仮定がおかしければ
もう片方が正解と分かる。
・候補が少なくなったら、式に頼らず作業して答えを見つける。

次回もよろしくお願いします。