みなさん、こんにちは。受験Dr.の亀井章三です。

 

今回も調べるのが大変な単元「場合の数」で、作業を楽にして解きやすくする３つのコツについてのお話しです。場合の数の問題では、樹形図や表を用いて調べることを要求する問題も入試で多く出題されます。せっかく解き方が分かっていても、作業の段階でミスをしてはもったいないです。３つのコツを用いて、作業でミスを減らし確実に正解を求められるようになりましょう。

 

2 樹形図は全部描かない　です。

　まずは次の問題をご覧ください。

 

問題　１から５までの数字がそれぞれひとつだけ書かれた封筒とカードがあります。

　　　　これらのカードを封筒の中に一枚ずつ入れるとき、封筒の数字とカードの数

　　　　字が一組だけ同じになるような入れ方は何通りありますか。

 

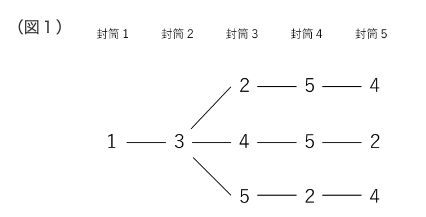
まずは「１の封筒に１のカードを入れる場合」を考えて樹形図を描きます。

２の封筒には同じ数字のカードを入れられませんので、３か４か５のカードが入り

ます。そこで、３のカードを入れた場合を考えます。以下、３、４、５の封筒にも、

封筒の数字と異なる数字のカードが入るように注意しながら樹形図を描きます。

（図１）

 

　次は、２の封筒に４のカードを入れた場合ですが、この樹形図は描く必要がありま

　せん。なぜなら、１の封筒に１のカードを入れた時点で、残った数字は全て封筒と

　カードに同じ番号が残っているという点で「同じ条件」だからです。

　２の封筒に３のカード　→　数字２はカードのみ、数字３は封筒のみ

　　　　　　　　　　　　　　　　　　数字４と５はカードと封筒の両方

　２の封筒に４のカード　→　数字２はカードのみ、数字４は封筒のみ

　　　　　　　　　　　　　　　　　　数字３と５はカードと封筒の両方

　このように、数字は異なっていても条件は等しいわけです。

　そのため、２の封筒に４のカードを入れたときの入れ方は、３のカードを入れたときと

同じ３通りになります。５のカードを入れたときも３通りです。

　したがって、１の封筒に１のカードを入れたときの入れ方は３×３＝９通りです。

 

　残ったカードが全て同じ条件のときは、１つの場合だけ樹形図を描いて調べ、残り

　はかけ算を用いて求めます。そうすると時間も短縮され、ミスも減ります。

 

　さらにもう一工夫をすると時間短縮することができます。

　今度は１の封筒に２のカードを入れる場合を考えます。先ほどの説明から、３の

カードを入れても、残った数字の条件は等しくなっています。

（カードのみの数字１つ、封筒のみの数字１つ、両方にある数字２つ）

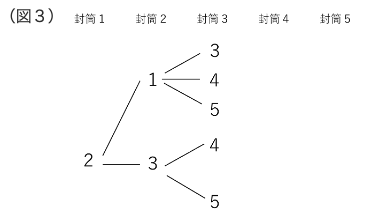
　したがって、２のカードを入れた場合の樹形図だけを描いて考えます。

　３の封筒まで入れた状態が（図３）です。

 

 

なお、２の封筒に４のカードを入れた場合も５のカードを入れた場合も、３のカード

を入れたときと同じ条件になりますので省略しています。また、２の封筒に３、３の

封筒に２を入れると、残ったカードが４と５になり、「１つの封筒だけ同じ数字が入

る」という条件を満たさないので描いていません。

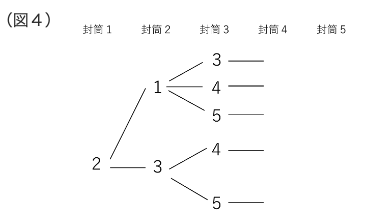
この後は、４の封筒、５の封筒に入れるカードを樹形図に書いていくのですが、

その入れ方が何通りかさえ分かれば、実際に何の数字が入るかを書かなくても

組み合わせを求めることができます。要は樹形図の「枝」の本数を数えることが

出来れば、どんな「葉」がついているかは関係ないということです。（図４）。

 

 

　これで、１の封筒に２のカードを入れたときの入れ方は、３＋２×３＝９通りと求め

　ることができます。３～５のカードを入れたときも同じ９通りのため、９×４＝36通り

　１のカードを入れたときが９通りでしたので、全部で９＋36＝45通りとなり、これが

　答えになります。

　この問題は他にも解き方がありますが、今回は樹形図の描き方のコツを伝えるこ

　とがテーマのため、丁寧に調べていく方法で解きました。同じものや必要ないもの

　をうまく省略することで、作業時間を短縮できるということです。

 

　ということで２番目のコツは、

１  条件が同じ場合は樹形図を省略して時間短縮することができる

２  残った並べ方が１通りしかない場合は、枝だけ描けば早く数える

ことができる　という時間短縮のコツでした。

 

次回は、「表を用いて場合の数の規則を調べるコツ」の話です。お楽しみに。