みなさん、こんにちは。受験Dr.の亀井章三です。

今回も調べるのが大変な単元「場合の数」で、作業を楽にして解きやすくする３つのコツについてのお話しです。場合の数の問題では、樹形図や表を用いて調べることを要求する問題も入試で多く出題されます。せっかく解き方が分かっていても、作業の段階でミスをしてはもったいないです。３つのコツを用いて、作業でミスを減らし確実に正解を求められるようになりましょう。

今回のコツは
3 規則性型は表で解く　です。
場合の数の問題にも「規則性」が存在します。見分けるポイントは、
設問が進むにつれて、段々試行回数が増えているかどうか、です。
このような規則性を用いて解く場合の数の問題を「規則性型」と呼ぶことにします。

では次の問題をご覧ください。

問題　１、２、３の数字が書かれたカードがたくさんあります。これらのカードを左から
順番に次のルールにしたがって並べていきます。
ルール１　１のカードの右となりには２か３のカードを置く
ルール２　２のカードの右となりには３のカードを置く
（１）3枚のカードの並べ方は何通りありますか。
（２）6枚のカードの並べ方は何通りありますか。
（３）9枚のカードの並べ方は何通りありますか。

この問題ですが、樹形図という解法のみで解こうとすると、（１）はカードが3枚と少ないので問題なく解けるでしょう。
しかし、（２）（３）になると、どれだけ大きな樹形図を描かなければいけないのか、考えただけで手が止まります。そこで（２）（３）を効率良く解くための手段が「表」になります。具体的に解答を見ていきましょう。

（１）今回は樹形図ではなく、全て書き出して解きます。
１２３、１３１、１３２、１３３、２３１、２３２、２３３、３１２、３１３、３２３、３３１
３３２、３３３
答えは13通りです。

（２）（３）　ここからは「規則性」を使って解きます。どのような規則性を考えれば
良いかと言うと、右端の数字で分類した時の枚数になります。
そこで、規則を見つけるために表を作ります。データが少ないので、カード2枚の場合を書き出します。１２、１３、２３、３１、３２、３３　の6通りです。

表の項目は、「カードの枚数」「右端が１」「右端が２」「右端が３」「合計」です。

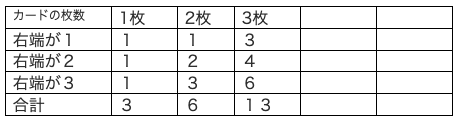
さあ規則は分かりましたか？ヒントはカードを並べる時の条件です。
１のカードは３のカードの右隣にしか並ばないので、□枚並べたとき右端が１になる並べ方は、（□－１）枚並べたとき右端が３になる並べ方と同じになります。
同様に、２のカードは１のカードと３のカードの右隣にしか並ばないので、□枚並べたとき右端が２になる並べ方は、（□－１）枚並べたとき右端が１になる並べ方と３になる並べ方の和になります。
そして、３のカードは１～３全てのカードの右隣に並ぶので、□枚並べたとき右端が３になる並べ方は、（□－１）枚の並べ方の合計と同じになります。

これをふまえて、表を9枚まで完成させます。

したがって、答えは（２）129通り、（３）1278通り　になります。

ということで３番目のコツは、
規則性のある場合の数の問題は、調べた結果を表にして解く
という規則性のコツでした。
3回に分けて場合の数の問題を効率よく解くポイントをお伝えしました。ぜひこれらのポイントを身につけて、スラスラと場合の数の問題を解けるようになってください。
次回もよろしくお願いします。