みなさん、こんにちは。受験Dr.の亀井章三です。

　今日は、中学校の数学で学習する「正負」の話を説明します。
－２のような「負の数」は、算数では学習しませんが、負の数の概念や
計算方法を知っていると、中学入試の問題を解くうえでも役に立ちます。
「負の数」の計算は決して難しいものではありませんので、ご安心ください。

１　負の数と足し算引き算

　１、２、３、４……のように、数えたり自然に存在する数のことを「正の数」というのに
対し、－１、－２、－３……のように、０より小さく数えられない（リンゴが－３個とは
言いません）数のことを「負の数」と言います。
要するに、「０より◎だけ小さくした数」のことを「－◎（マイナス◎）」と表現します。気温で「－３℃」というふうに使われます。これも「０℃」より３℃低いということになります。

この正負の数をとらえるときは数直線が便利です。
０から見て、数が増えると右に、減ると左に進みます。

つまり、「＋５」は０から５右に進んだ数、「－４」は０から４左に進んだ数になります。
この数直線を用いて、足し算引き算を考えます。

（１）正と正の足し算

これは今までやってきた計算と同じで、答えは必ず「正」になります。
例　（＋３）＋（＋２）
これは０から「右に３進んで」、さらに「右に２進む」という意味です。
結局「右に５進んだ」ことになるので、答えは＋５になります。
なお、正の数の「＋」は一般的には省略して書きます。

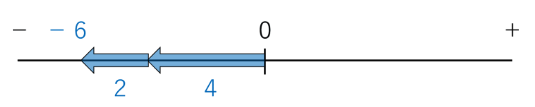
（２）負と負の足し算

では、負の数と負の数のたし算はどうでしょう。
例　（－４）＋（－２）
これは０から「左に４進んで」、さらに「左に２進む」という意味です。
結局「左に６進んだ」ことになるので、答えは－６になります。

（３）正と負の足し算

ということは、正の数と負の数の足し算は、「右に進む」と「左に進む」が
行われることになります。このとき、結局０から見て左右どちらにいるのかは
右と左それぞれどれだけ進むのか、より進むのはどちらなのか？ということ
が鍵を握ります。
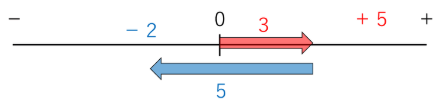
例　（＋３）＋（－５）
これは０から「右に３進む」そして「左に５進む」という意味です。
このとき、左に進む数の方が大きいので、結局０から左に進んだ「負の数」
が答えになります。３と５の差は２なので、０から左に２進んだ、－２が答え
になります。

　今回は、まず正の数と負の数とは何？というところから、具体的な足し算の話
までを説明しました。次回は「引き算」について説明いたします。お楽しみに。