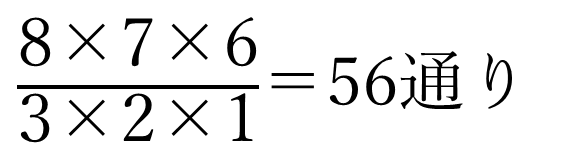皆さんこんにちは。

受験Dr.講師の勝山利信です。

今回のテーマは算数の「場合の数」の中でも、図形と場合の数を話題に考察力を高める話をします。

考察とは、物事を明らかにするために、よく調べ考えることを指しますが、算数の問題の中でも規則性に関する問題や場合の数に関する問題を解くときに必要な力ですね。考察力が培われていないと、与えられた数値をあまり考えもせずにいい加減に組み合わせて計算し、解答かのような数値をとりあえず出すというようなことに陥ってしまいます。また、しっかりと考察したつもりでも、間違えやすいポイントが隠れており、まさにそこにひっかかってしまい間違えるというようなこともあります。

それでは、具体的な問題を通して考察力を高めていきましょう。

 

似ているようで異なる問題

以前、次の問題と非常によく似た問題をもとに、場合の数についてお話したことがあります。

問題

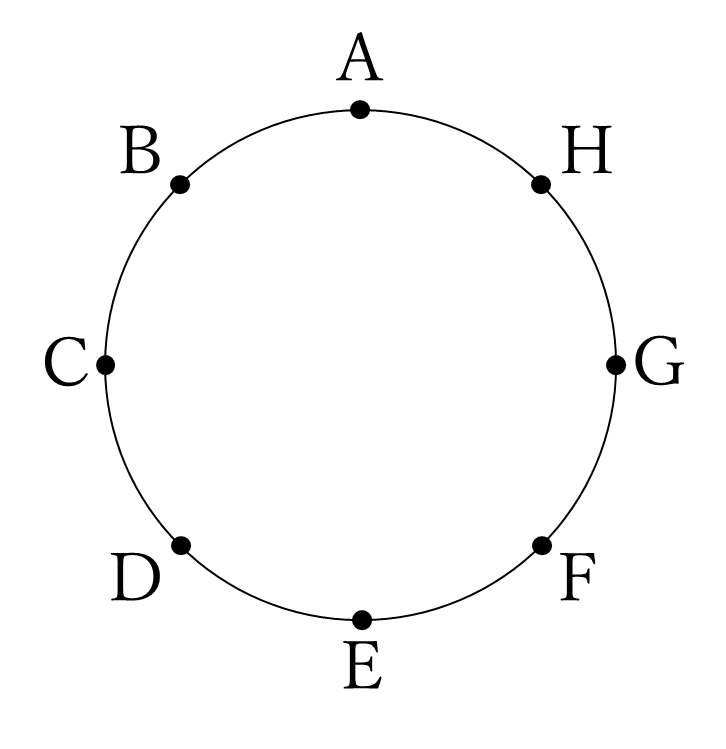
次の図のように円周を８等分するA～Hの８点があります。そのうち、３点を頂点とする三角形は何種類できますか。ただし、回転させたり、ひっくり返したりして重なる図形は１種類と数えます。

三角形が何通りできるか問う問題なのであれば、円周上では3点が一直線上に並ぶことが無いことを前提に、８点から３点選べば次々と三角形ができるので、組み合わせを求める式を用いて

より、56通りと計算できる、というお話を以前しました。

今回の問題は問題文をよく読み正確に問いの内容をとらえないと、この計算をして解き終わったような気がしてしまうので注意しましょう。

三角形が何種類できるか問われています。

さて、個数を数えることと種類を数えることは、何が異なるのでしょうか？

では、考察するために調べてみましょう！

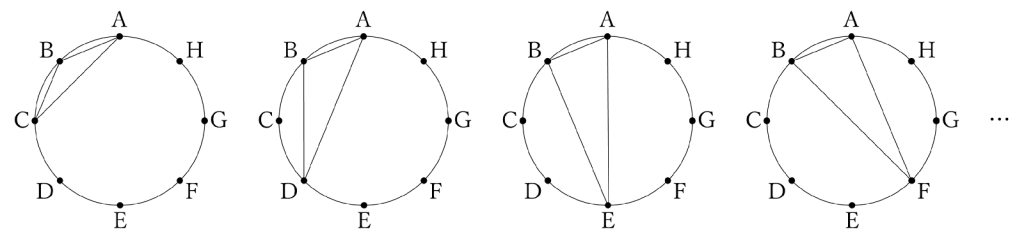
重複が無いようにアルファベット順に点を選んで三角形を書いていきます。

すると、３個目と４個目に同じ形で向きが異なる三角形ができます。これは１種類とするという考え方なので、このような同じ種類の三角形を何回も数えてしまわないように注意しなければならないことが分かります。

その注意点を守れば、全部で56個の三角形ができることは計算上分かっているので、56個の三角形を書いてから、何種類あるか数えることもできなくはありません。

「できなくはない」というのは、テストには時間制限があることを考えると現実的ではないということです。

では、どのようにすれば的確な時間で種類を数えることができるのでしょうか？

 

【数値化して考える】

今回は形を数値化して考えるという方法が有効です。図形と規則性に関する問題でも、同様に考える場面が多々あります。

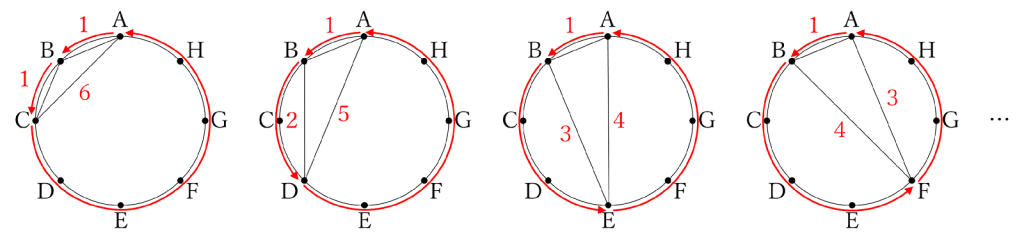
次の図のように、三角形の辺の近くに、何個分はなれた２点を結んだ辺なのかメモしてみます。

１個目は（１、１、６）、２個目は（１、２、５）、３個目は（１、３、４）、４個目は（１、４、３）となりました。

このように、円周を８等分している点を使って三角形を作るので、和が８になるように３つの数に分けると三角形の種類を簡単に考察することができます。すると、３個目と４個目は並ぶ順序が変わっただけなので、同じ種類の三角形であることの判断もしやすくなります。

これで、この問題を解くためにするべきことが見えてきました。

和が８になるように３つの数に分けると、

（１、１、６）、（１、２、５）、（１、３、４）、（２、２、４）、（２、３、３）の５通りが考えられるので、これにしたがって３点の間をあけて辺を書けば５種類の三角形ができると解答できます！

このように、「まずは地道に調べる→調べたことをもとに作業量を減らせないか考える」というように頭を働かせるようにし、それに伴う調査や計算のトレーニングをすると考察力が身につきます。ただし、テストの最中に調べる時間を十分に確保できるわけではないので、よく出題される問題については可能な限り類題の考察を事前に行ってテストに臨めるようにしましょう！

次回はさらに深い考察が必要になる問題についてお話したいと思います。

目指せ考察力UP！

それでは、またお会いしましょう！