皆さんこんにちは。

受験Dr.講師の勝山利信です。

 

前回に引き続き、算数の「場合の数」の中でも、図形と場合の数を話題に考察力を高める話をします。

～前回のポイント～

考察＝『物事を明らかにするために、よく調べ考えること』

⇒まずは地道に調べる→調べたことをもとに作業量を減らせないか考える

 

さて、今回はこのポイントを元により深い考察が必要になる問題についてお話します。

早速、具体的な問題を見てみましょう！

 

問題

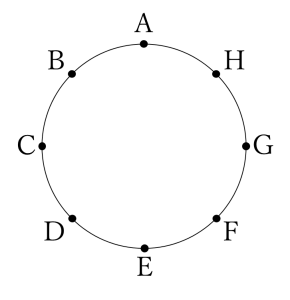
次の図のように円周を８等分するA～Hの８点があります。そのうち、４点を頂点とする四角形は何種類できますか。ただし、回転させたり、ひっくり返したりして重なる図形は１種類と数えます。

 

前回が３点を選び三角形を作る問題だったのに対して、今回は４点を選び四角形を作る問題へと発展しました。

地道に調べて考えるというスタートの切り方は同じです。

円周を８等分している点を使って四角形を作るので、和が８になるように４つの数に分けると四角形の種類を考察することができます。重複が起こらないように書き出してみると、

①（１，１，１，５）

②（１，１，２，４）

③（１，１，３，３）

④（１，２，２，３）

⑤（２，２，２，２）

というように、５パターンの分け方があることが分かります。三角形を作る問題であれば、この書き出した結果から５種類作ることができると答えて問題ありませんでした。

 

それでは、深く考察してみましょう。

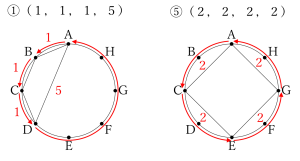
①、⑤は実際に四角形を書いて見ると、

というように、１つの四角形がそれぞれ描かれます。

 

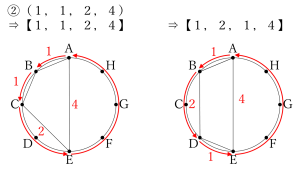
②はどうでしょうか？

こちらは書き出してみると、数の順番を入れかえることにより異なる四角形が作られるので、作ることのできる四角形は２種類であることが分かります！

まとめると、

①（１，１，１，５）⇒【１，１，１，５】のみ

②（１，１，２，４）⇒【１，１，２，４】、【１，２，１，４】の２種類

③（１，１，３，３）⇒【１，１，３，３】、【１，３，１，３】の２種類

④（１，２，２，３）⇒【１，２，２，３】、【１，２，３，２】の２種類

⑤（２，２，２，２）⇒【２，２，２，２】のみ

合計８種類の四角形を作ることができることがわかりました！

 

三角形を作る問題から四角形を作る問題に条件を変わることで、より深く考察する必要があったわけですね！

このように、一見同じように見える問題でも、条件の違いによって考察する深度は変化します。

やはり、テストを受ける前に類題の考察を行う学習をしておくべきですが、得点化できる問題の幅を広げるだけでなく、試験時間内に作業を完了できるのか冷静に判断するためという意味合いもあります。

調査する必要のある問題は完了しなければ得点化できないので、解くならテキパキ最後まで行うか、残り時間と照らし合わせた結果その問題は解かないと判断するかどうかもトータルの得点に大きく影響します。

是非、算数に必要とされる力を身につけたうえで、試験時間を有効に使えるようにするためのトレーニングも積んでいきましょう！

目指せ考察力UP！

それでは、またお会いしましょう！