皆さんこんにちは。
受験Dr.講師の勝山利信です。

今回のテーマは「ばねの伸び方」です。
ばねは力をかけると伸びたり縮んだりするという性質をもっています。
その伸び縮みの長さが加えた力の大きさ（つるしたおもりの重さ）に比例することから、計算を含む問題として出題するのに丁度良く、中学入試の問題でもよく題材になります。

仕組みはシンプルですが、伸び縮みの原因になっている力は目に見えません。
そのため結果の方から起こっていることをイメージするという難しさがあります。
また、ばねの組み合わせ方によって難度の高い問題から低い問題まで幅広く出題できます。
典型的な組み合わせを理解することから始め、入試で出題されるような複雑な組み合わせにも対応できるように理解を深めていきましょう！

基本的な性質～ばねが伸びるということ～

基本的な性質はシンプルで、このことを知識として定着させることはそれほど難しくはありません。ただし、ばねの長さを問う場合と伸びの長さを問う場合があるので、自分の解答が問いの内容からずれないように注意しましょう。

一般的にばねに関する問題が出題されるときは、つるしたおもりの重さによってばねの長さがどのように変化するかについて表やグラフが与えられます。今回は表を使います。

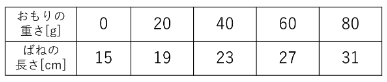
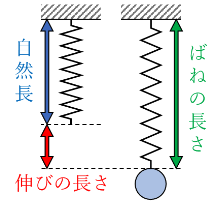
ばねのもともとの長さのことを自然長といいます。おもりの重さが0gのときのばねの長さが15cmなので、このばねの自然長は15cmです。また、おもりの重さが20g大きくなるごとにばねの長さが4cm増えているので、このばねは1cm伸ばすのに5gの力が必要であることが分かります。自然長と伸ばすのに必要な重さ、この２つの数値をしっかりと押さえておけば、基本的な問題を解くことは十分にできます。

さて、ここで注目してほしいことは、そもそもばねが伸びるということはどのような現象なのかということです。
数値だけに注目してしまい計算方法を機械的に覚えるような姿勢で学習してしまうと応用的な問題に太刀打ちできなくなってしまうので、このタイミングで根本原理を是非押さえましょう！

ばねは「柔軟性があり、もとの形に戻ろうとする力が適度にはたらく物質」でできています。
様々な物質でつくることはできますが、性質が適しているので主に金属で作られています。問題に出題されることは稀ですが、金属でできたばねでも極端に強い力で引っ張るとピンッと張った針金のようになってしまいもとの形には戻らなくなります。普段は、元の形に戻る範囲の力の大きさで出題されていると言えます。

そして、ばねが伸びるときの様子を見てみると小さな伸びが積み重なっていることが分かります。
次の図で確認しましょう。

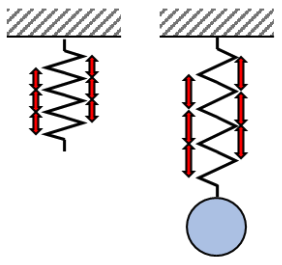
おもりをつるすと１つ１つの間隔が広がり、その広がりが積み重なってばねは伸びます。
問題として出題されているときは伸びの前後で間隔の個数が異なっている場合もありますが、これは図を簡易化しているだけなので気にしないようにしましょう。

このことを踏まえて次の問いについて考えてみましょう。
ばねの仕組みを理解できると、このような問いの答えをただ単に暗記するのではなく、物事として正しくとらえることができるようになり、忘れにくくなります。

問い：ばねAを半分に切りばねBをつくりました。ばねAとばねBでは、どちらが強いばねですか？

２種類のばねを用いた問題を出題する際に、このような条件が登場します。
強いばねとは、力をかけても変形しにくい伸びにくいばねのことです。
「半分に切る→短くなる、弱くなる」というようなマイナスのイメージがつながりそうですが、実は切った後のばねBの方が強いばねになります。

先ほど表で数値資料を与えたばねをばねAとするのであれば、
ばねA：自然長15cm、20gで4cm伸びる→5gで1cm伸びる

このようなばねを半分に切ることで、
ばねＢ：自然長7.5cm、20gで2cm伸びる→10gで1cm伸びる

1cm伸ばすのに必要な力が5gから10gに増えていることが分かります。

ばねの伸びが小さい伸びの積み重ねであるとイメージできれば、半分に切ることで間隔の個数が減り、伸びの量が減ることが分かります。伸びにくくなるということは、強いばねということですね。

数値を答える問題の学習で重要なこと

中学受験の理科では、物事として理解を深めて判断力を身につけることと、機械的な数値処理を的確に速く行うことの両方が求められます。基礎的な一問一答式の問題で問われるような内容が、難問を解く際に必要な理解力につながることもあるので、将来的に得点化するための力を身につけることを意識しながら学習を進めましょう。次回は、ばねの組み合わせ方による考え方と具体的な数値処理の方法についてお話します。

目指せ理解力UP！
それでは、またお会いしましょう！