皆さんこんにちは。
受験Dr.講師の勝山利信です。

前回のブログでは、面積の単位であるａ(アール)やha(ヘクタール)について、具体的な広さのイメージを持つことで知識の定着が良くなることについてお話しました。
今回はそこから発展させて「縮尺と面積」についてお話します。

模試や入試においては、１回分の算数のテストで出題されたとしても１問程度です。その問題ができてもできなくても影響は小さいと思ってしまいがちですが、基本的な処理力を問う問題を確実に得点化していくことは、成績を安定させるためには非常に重要なことです。

 

縮尺と面積の問題の正答率はなぜ低いか？

地図を作るときは、実際の大きさから縮めて道や土地、建物を表します。
その縮めるときの度合を縮尺といいます。実際の長さに対して地図上の長さがどのくらい縮んだのかを表すので、例えば・・・

実際の長さが2kmの道を地図上では4cmで表したとすると、
2km　→　2×1000×100＝200000cm　　200000÷4＝50000より、
50000分の1の大きさにして地図に表したことになります。

そのように作った地図では、読み取った長さを50000倍すると元の長さに戻せるということですね。
このことは割と理解できる人が多いので、長さについて計算する縮尺の問題は正答率が高くなります。

これが面積の話題になったとたんに正答率がガクっと低くなります。
これは、大きさを拡大した縮小したりするときのとらえ方にあやふやさが残ってしまっているからです。

もう一度確認すると、縮尺は「長さ」の拡大・縮小の倍率を表しています。
「面積」の拡大・縮小の倍率を直接表していないことをはっきりさせておきましょう！

 

イメージを持ってトレーニング

あやふやさを無くすためにすることですが、まずは具体的な図を書いてトレーニングすることをお勧めします。算数が苦手な人ほど結果を早く求めようとする傾向があるので、あせらずにきちんと足元を固めることを意識して練習しましょう。

～例題①～
縮尺が50000分の1の地図上で30c㎡の土地の広さは、実際には何k㎡ですか。

ゴールは問われているように何k㎡か答えることですが、まずは「地図上で30c㎡の土地」をしっかりとイメージしましょう。形は指定されていませんが、長方形にするとシンプルです。
30c㎡の長方形の縦・横の長さは様々な組み合わせが考えられますが、面積が30c㎡であれば問題ありません。例えば、縦5cm、横6cmの長方形で考えてみましょう。

先ほど確認したように、縮尺は長さの拡大・縮小の倍率を表しているので、それを踏まえてたてと横の長さをそれぞれ実際の長さに戻してみましょう。

縦　5×50000＝250000cm　→　250000÷100÷1000＝2.5km
横　6×50000＝300000cm　→　300000÷100÷1000＝3km

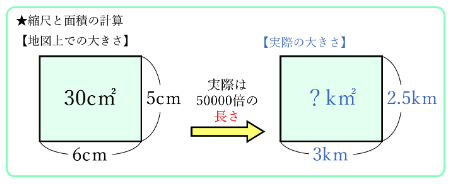
よって実際の広さは、2.5×3＝7.5より7.5k㎡となります。

縮尺が長さの拡大・縮小の倍率であることをしっかりとイメージせずにあやふやにしたまま解くと、
＜間違えた解き方の例＞
30c㎡×50000＝1500000c㎡　(縮尺の分の倍率をかけて、もと大きさに戻して・・・)
1500000÷100÷1000＝15k㎡(cm → m → kmに換算して・・・できた！)
というように、間違えてしまいます。

 

理解出来たら機械的な処理で時間短縮！

どのような仕組みで実物と地図との間で面積の換算が行われるのか理解することができたら、次のステップとして機械的な処理で計算時間の短縮を図りましょう！

先ほどの計算を分数の形を使って１つにまとめるとスッキリします。

条件を確認してから、このような形で式を立てることができれば、あとは冷静に約分をして計算結果を出すだけとなります。

この形を使うと、逆の作業も楽になります。

～例題②～
60haの土地は縮尺が20000分の1の地図上では何c㎡の大きさで表されますか。

haから㎡への換算は別に計算しておきましょう。
1ha＝10000㎡ですから、60×10000＝600000より600000㎡となります。
では、分数の形でまとめてみます。

約分して整理すると最後は60÷4が残り、地図上での面積は15c㎡であると求められます。

 

テストは時間制限あり！

テストでは処理する能力が問われるため短時間で結論を出す必要があります。面倒な計算処理をしなければならない場面では、今回のように型を決めておいて取り組むとスムーズに処理できます。式を暗記しあてはめるわけではないので気を付けましょう。肝心なことは理解したうえで、型を上手く使うためのトレーニングを積むことです。

目指せ計算処理力UP！
それでは、またお会いしましょう！