みなさん、こんにちは。
受験ドクター算数・理科科の川上と申します。

本日はタイトルの通り、完全中和点を求める問題の解法を紹介いたします。

［問題］
ある濃さの塩酸4㎤を蒸発皿に入れ、BTB溶液を加えました。それぞれにある濃さの水酸化ナトリウム水溶液を加えて色を調べ、さらに蒸発皿から水分を蒸発させ、残った固体の重さをはかりました。塩酸4㎤と過不足無く反応する水酸化ナトリウム水溶液は何㎤ですか。以下の表をもとに答えなさい。

[解説]
BTB溶液の色を見ると、CとDの間に完全中和点があります。ちなみに、「BTB溶液の色」というヒントが無ければ、変化率で完全中和点を予測することになります。

さて、このような完全中和点が表の中に無い問題では、多くの参考書で「つるかめ算」を利用して解く方法が紹介されています。解法自体はとても明快ですが、計算が煩雑になることが多いのが欠点です。
今回はグラフを利用した解法を紹介します。

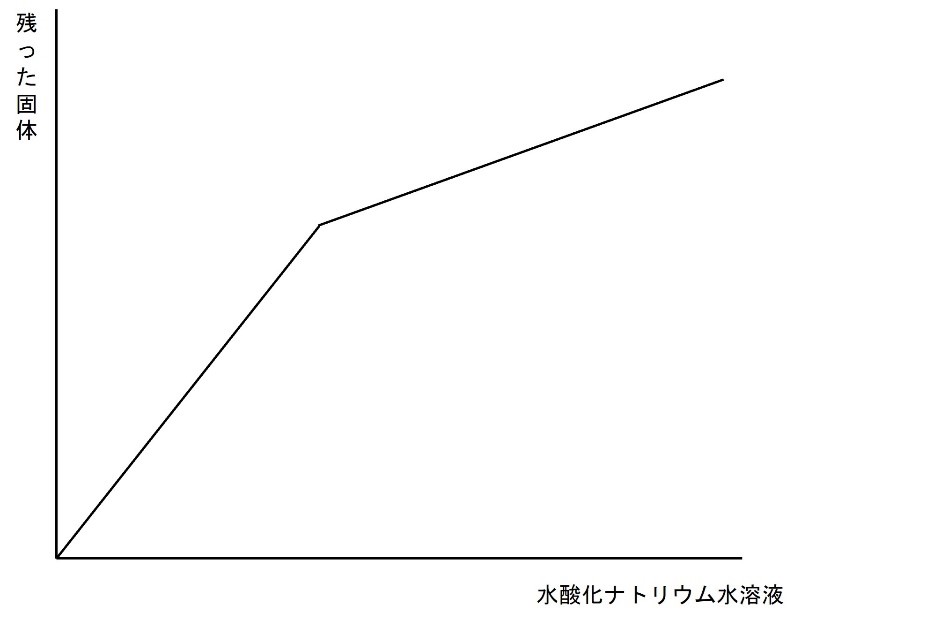
グラフの概形は見たことがある子が多いと思います。
ここでは完全中和の前後であるＣとＤ、そしてＥについて残った固体の量を記入します。

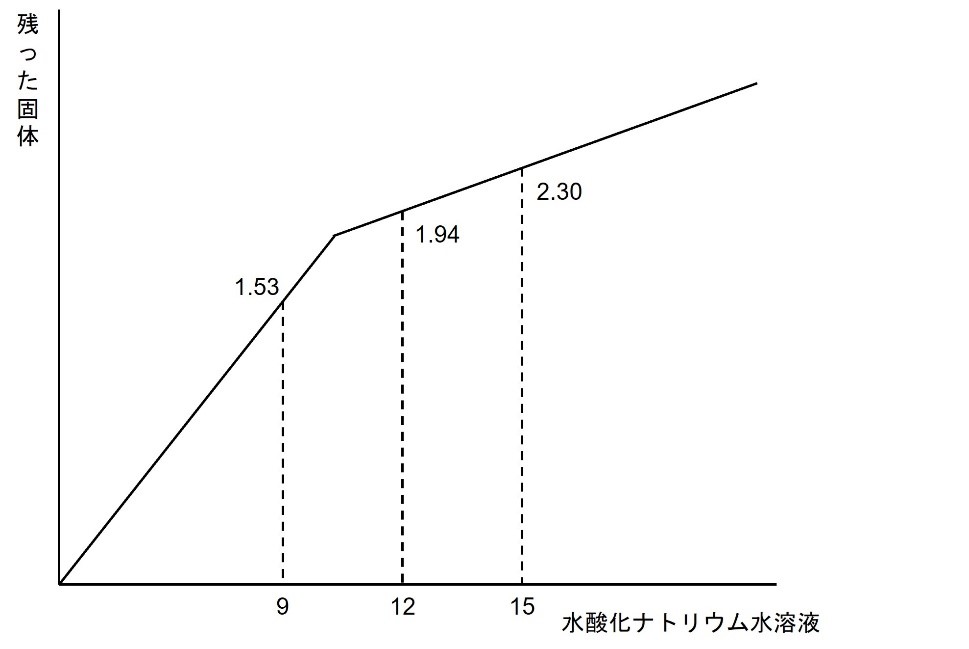
次に、以下のように完全中和前の直線を延長します。

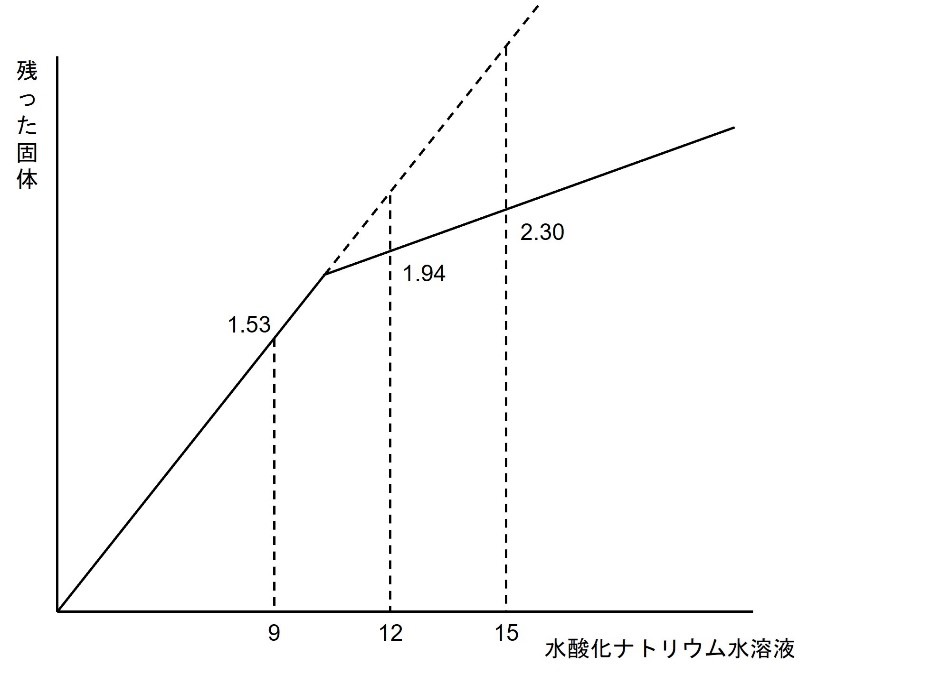
完全中和前は、水酸化ナトリウム水溶液3㎤あたり0.51ずつ固体が増えています。
完全中和していなければ、水酸化ナトリウム水溶液12㎤のときに0.51×4＝2.04
水酸化ナトリウム水溶液15㎤のときに0.51×5＝2.55となります。
その値をグラフに記入しておきます。

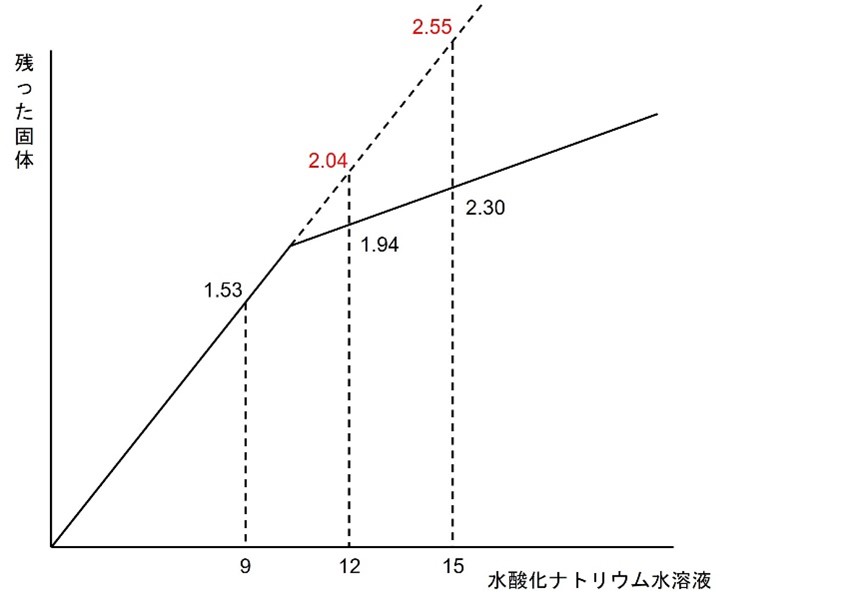
以上で下準備は終わりです。
ここで、以下の三角形の相似に注目します。

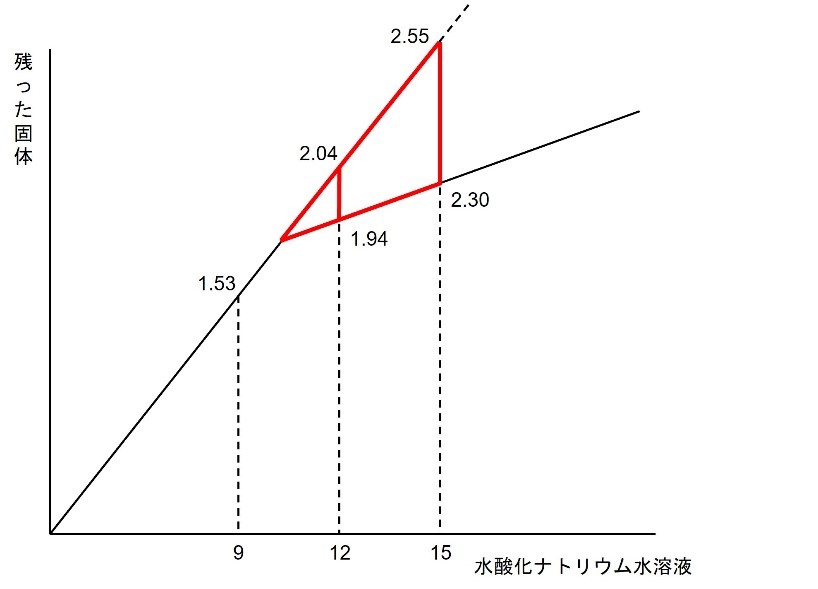
2.04－1.94＝0.1
2.55－2.3＝0.25

より、以下の図のように辺の長さが定まります。

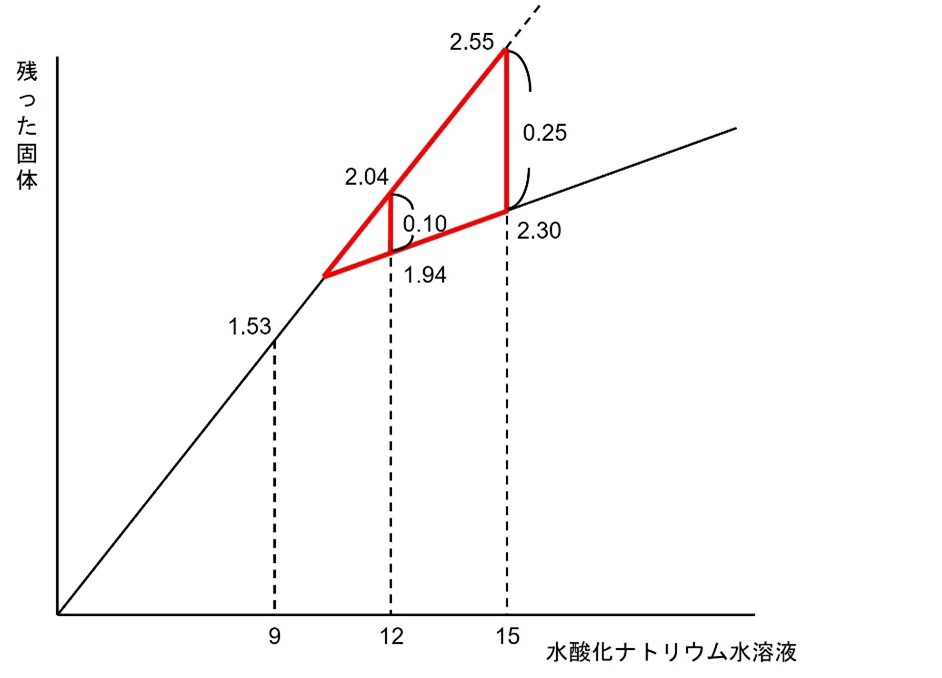
0.1:0.25＝2:5より、横軸の長さの比が以下の図のように定まります。

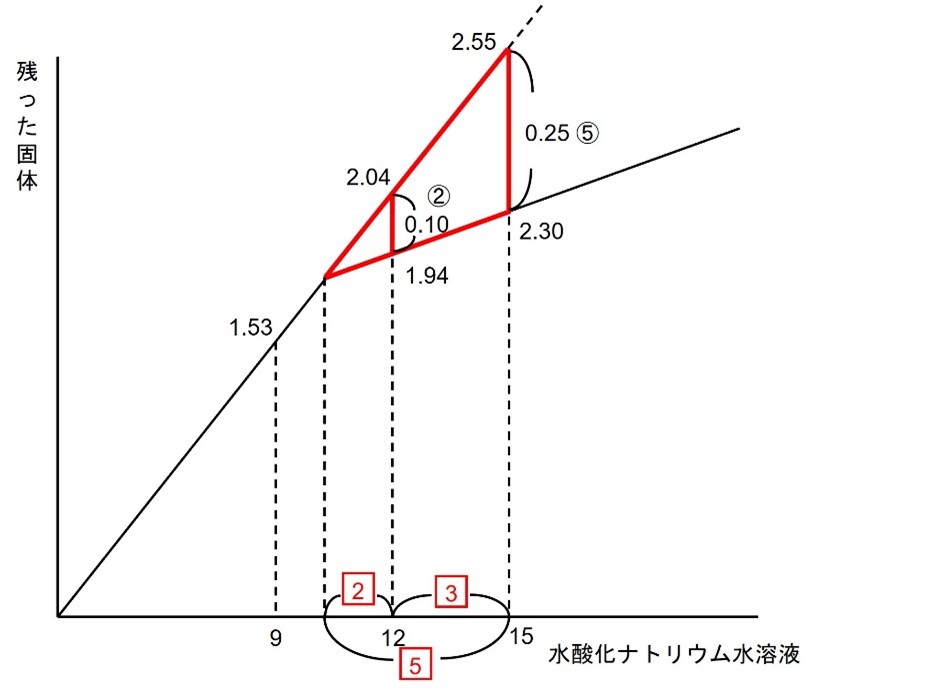
３＝15－12＝3より、１＝1となるので、２＝2
よって12－2＝10となります。

順に説明しましたので図が多く、大変そうに見えるかもしれませんが計算量をかなり減らすことのできるおすすめの解法です。是非ご活用ください。

それでは、失礼いたします。

受験ドクター　川上亮