みなさん、こんにちは。
受験ドクター算数・理科科の川上と申します。
前回、シェルピンスキーのギャスケットと呼ばれるフラクタル図形の問題を紹介しました。今回はフラクタル図形の仲間である「コッホ曲線」について触れたいと思います。
作り方は以下の通りです。
線分を用意します。
![]()
3等分します。
![]()
中央に正三角形を作り、下の辺を消します。

各辺を3等分します。

中央に正三角形を作り、下の辺を消します。

これをくり返していくと、図形の一部が全体と相似なフラクタル図形となります。
実際の入試問題を見てみましょう。
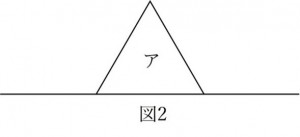
下の図1のように、1本の長い線を書きました。この線を3等分して、その真ん中の部分にその長さを1辺とする正三角形アを図2のように書き足しました。次に、図2において、正三角形アの2辺をそれぞれ3等分して、真ん中の部分にその長さを1辺とする正三角形イ、ウをそれぞれ書き足しました。さらに、正三角形アの両側の部分も3等分して真ん中の部分にその長さを1辺とする正三角形エ、オをそれぞれ図3のように書き足しました。次に図3において正三角形イの2辺をそれぞれ3等分して真ん中の部分にその長さを1辺とする正三角形を書き足し、正三角形イの両側の部分も3等分して、真ん中の部分にその長さを1辺とする正三角形を書き足します。同様に正三角形ウ、エ、オに対してもそれぞれに同じ作業を行うと図4のようになります。図2で正三角形アの面積は2916㎠です。次の問いに答えなさい。【2012立教女学院中 一部省略】
(1)省略
(2)図4において、同じ作業をもう一度行ったあとのすべての三角形の面積の和は何㎠ですか。
![]()


【解説】
正三角形の個数と、次の操作で分割される辺の数についてまとめてみます。
「次の操作で分割される辺」とは、例えば図3であれば下の図の赤線です。

また、相似比と面積比の関係より、新しくできる正三角形の面積は1/9倍になっていきます。
図2の正三角形の面積を1とし、図3までまとめたものが以下の表となります。

様々な規則が見えてきますね。
たとえば、図3の三角形の個数は、図2の三角形の個数に、次の操作で分割される辺の本数の和となっています。

また、図3の次の操作で分割される辺の本数は、図2の4倍になっています。

図形の変化を考えても、この規則には気付くことが出来たかもしれませんね。
図5まで表を埋めたものが以下となります。

増えた三角形の個数、面積に注意して計算すると
2916×(1+1/9×4+1/81×16+1/729×64)=5044㎠
となります。
最近はあまり見かけなくなりましたが、図形の変化や表の数値から規則を考える練習としてはとてもいい題材かと思います。
ご参考になれば幸いです。
それでは、今回はここで失礼します。
受験Dr. 川上亮




