みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

今回はタイトルの通り、2024年度入試の開成中の問題を紹介できればと思います。

今年度の開成中、算数においてはとにかく大問１の(1)が話題となりました。
確かにインパクトが強かったですよね。受験生たちも四苦八苦したのではないでしょうか。

私が今回紹介したいのは、大問１の(2)です。

【問題】
2本の金属棒O、Pがあります。長さはPの方がOより2㎝長く、重さは2本とも同じです。長さ1㎝あたりの重さは、Oはどこでも1㎝あたり10gです。Pは、中間のある長さの部分だけ1㎝あたり11gで、それ以外の部分は1㎝あたり8gです。

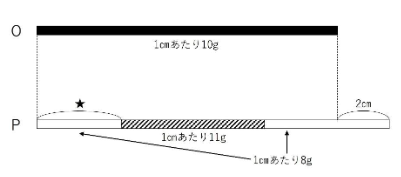
2本の金属棒を図の左端から同じ長さだけ切り取るとすると、切り取る部分の重さが等しくなるのは、切り取る長さが34.5㎝のときだけです。

(ア)図の★の部分の長さを求めなさい。
(イ)金属棒1本の重さを求めなさい。

この問題を紹介したい！と思ったのには理由があります。
近年の最難関校のトレンドとして、思考力を試す問題の増加が挙げられます。
条件を整理し、試し、本質に近づき、解答にたどり着く問題として、とても良い問題だと感じました。

【解説】

(ア)金属棒Oは1㎝あたり10gだとわかっているため、34.5㎝の重さは345gです。
よって、金属棒Pの★の部分と、1㎝あたり11gの中間部分の一部の重さの和が345gとなるはず。

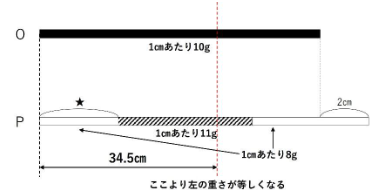
つるかめ算より、★＝11.5㎝とわかります。

※何かおかしくない？と思った方、いらっしゃると思います・・・（とても鋭いです）
が、とりあえず先に進みます。

問題は(イ)です。

私はこの問題を初めて解く際に、金属棒OとPの重さの変化をグラフにしました。
以下のようなグラフです。

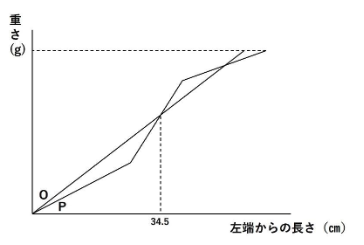
ただ、ここで違和感に気付きました。

重さが等しくなるところが2か所出てきてしまいます。

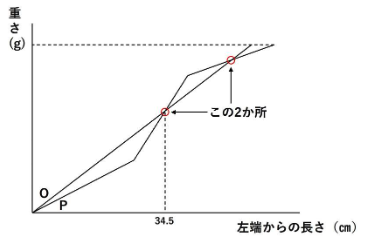
「2本の金属棒を図の左端から同じ長さだけ切り取るとすると、切り取る部分の重さが等しくなるのは、切り取る長さが34.5㎝のときだけ」

という条件に反します。

ここで強く違和感を感じ、どこに原因があるのかを考えました・・・

↓↓↓

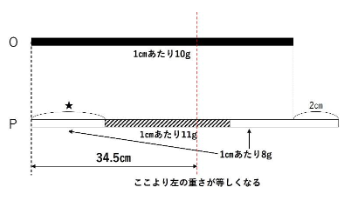
この図だ！

斜線部分の途中で金属棒Pを切断していたけれども、この下の図のように切ったから重さが等しくなるところが1か所なんだ！

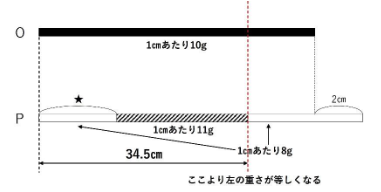
(ア)で違和感があった方、お付き合いいただきありがとうございます(笑)

つまりグラフは以下のようになります。

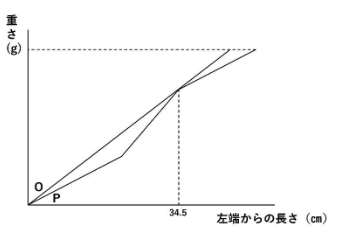
気付いてしまえばあとはカンタン。答えは425gとなります。

※補足

ちなみに、切り方はもう1パターン考えられます。
以下のように、1㎝あたり11gの範囲の右側で切ってみましょう。

「切り取る部分の重さが等しくなるのは、切り取る長さが34.5㎝のときだけ」という条件をもとにグラフを描いてみます。
無理矢理34.5㎝のところで重さを等しくしようとすると・・・

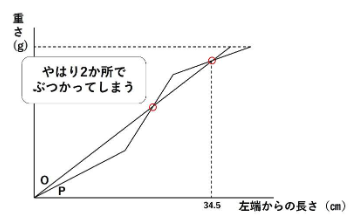
というわけで、この切り方も条件を満たさないわけです。

試行錯誤をしながら問題の本質に近づいていく感覚、いかがでしたでしょうか。

本当に算数って楽しいし面白い！そう思わせてくれる問題だと思います。

少しでもご参考になる点があれば幸いです。

それでは、今回はこれで失礼します。

受験Dr.　川上亮