みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。
年も明け、2025年となりました。本日が入試初日という受験生も数多くいるでしょう。
2025年はなんと1936年以来、89年ぶりの平方数(45×45)の年です。他にも「2025」という数字には様々な性質があります。
ここで基本的な知識をおさらいしておきましょう。
1 素因数分解の利用
2025を素因数分解すると、以下のようになります。
2025=3×3×3×3×5×5
それでは2025の素因数分解を利用した問題に触れてみましょう。
【問題】
(1)2025の約数の個数を求めなさい。
(2)2025の約数の総和を求めなさい。
【解説】
いずれも公式の活用がテーマですね。
(1)素因数3の使い方が0~4の5通り、5の使い方が0~2の3通りです。
よって、3×5=15通りが答えとなります。
(2)素因数分解の形より、約数の和は以下のようになります。
(1+3+9+27+81)×(1+5+25)=3751
公式を忘れていたのであれば、必ず確認しておきましょう。
2 2025=45×45の利用
以下の数表において、次の問いに答えなさい。
(1)1行45列の数字を求めなさい。
(2)46行1列の数字を求めなさい。
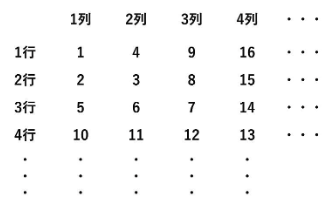
【解説】
(1)1行には四角数(平方数)が並んでいますね。
45列目は45×45=2025となります。
(2)1列には(1)で利用した四角数に1を足した数値が並んでいます。
1列46行は2025の次の数であるため、2025+1=2026です。
3 2025=1+3+5+・・・+89の利用
1からの連続する奇数の和は四角数となるため、②と共通する考え方を使うこともありそうです。
【問題】
以下のようにある規則に基づいてご石を並べていきます。
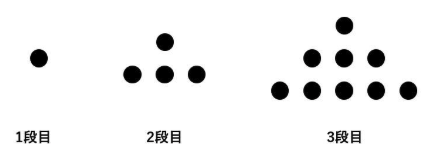
(1)一番下の段が89個になるように並べたとき、必要なご石の数は何個ですか。
(2)(1)の状態から、ご石をすべて集めて正方形の形に並べ直します。このときの正方形の一番外側には何個のご石が並んでいますか。
【解説】
(1)知っていればすぐ答えが出せますね。
1+3+5+・・・+89=2025です。
※「何番目の奇数になるか」は素早く導き出せるように練習しておきましょう。
89は、以下の計算より45番目の奇数となります。
(89+1)÷2=45
(2)2025=45×45より、1辺に45個のご石が並ぶことになります。
(45-1)×4=176です。
4 2025=(1+2+3+4+5+6+7+8+9)×(1+2+3+4+5+6+7+8+9)の利用
やや複雑になってきました。45が1~9の三角数になっていることと、2025=45×45を利用した考え方になります。
【問題】
(1)九九の2の段の答えを全て足すといくつになりますか。
(2)九九の7の段の答えをすべて足すといくつになりますか。
(3)九九の1の段~9の段までの答えをすべて足すといくつになりますか。
【解説】
(1) 2×1=2、2×2=4、・・・2×9=18のすべての和を求めます。
2×1+2×2+・・・・+2×9
=2×(1+2+・・・9)
=2×45
=90
より、90が答えとなります。
(2)(1)と同様です。
7×(1+2+・・・9)
=315
より、315が答えですね。
(3) (1)や(2)の計算過程を利用します。
例えば2の段は
2×(1+2+・・・9)=2×45
でしたね。
同様に、3の段は3×45、4の段は4×45になります。
よって、1~9の段の答えの合計は
1×45+2×45+3×45+・・・+9×45
=(1+2+・・・9)×45
=45×45
=2025
より、答えは2025となります。
基本的な知識・解法の確認でしたが、いかがでしたでしょうか。
(立法数の和に関する問題にも触れたかったですが・・・)
抜けていた知識があれば、是非覚えておきましょう。
皆さんが全力で中学入試に立ち向かう姿を心から応援しています。
それでは、今回はここで失礼します。
受験Dr. 川上亮




