みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。
本日は、生徒から受けた質問の中から平面図形の問題を紹介します。
その中で、補助線の引く上での考え方について触れていきます。
【問題】
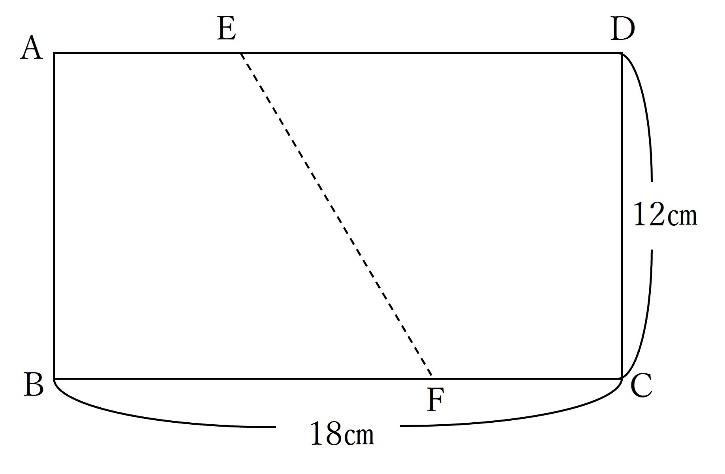
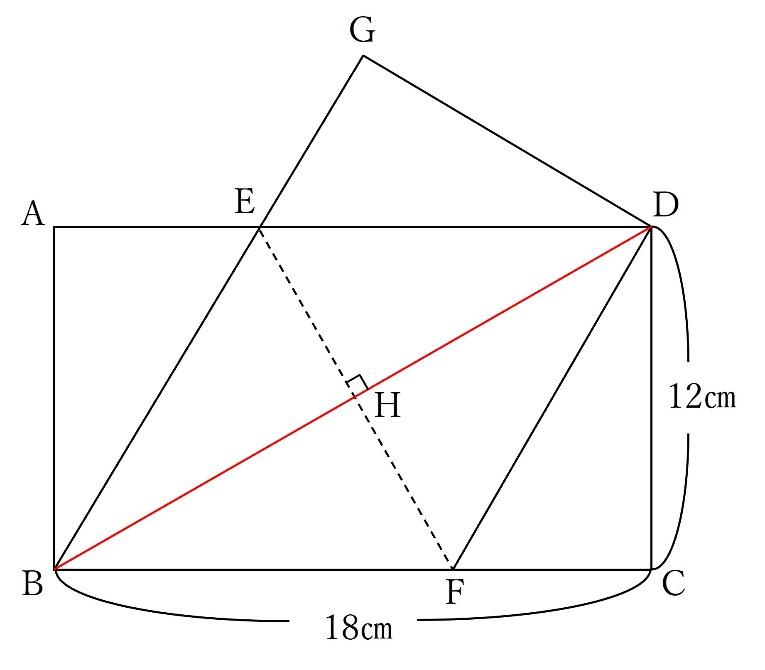
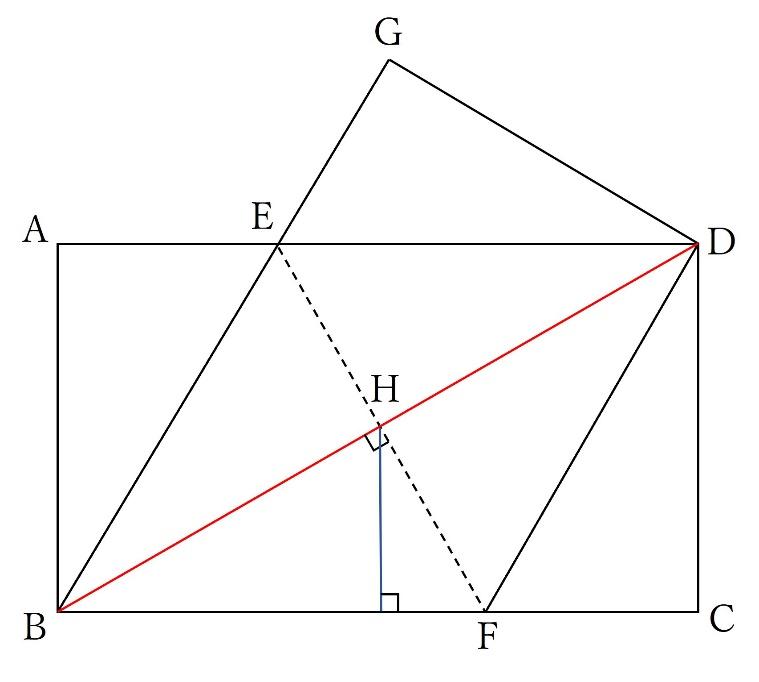
下の図のような長方形ABCDがあります。この長方形を、点Bと点Dが重なるよう、EFを折り目にして折り返します。
このとき、四角形EBFDの面積を求めなさい。
【解説】
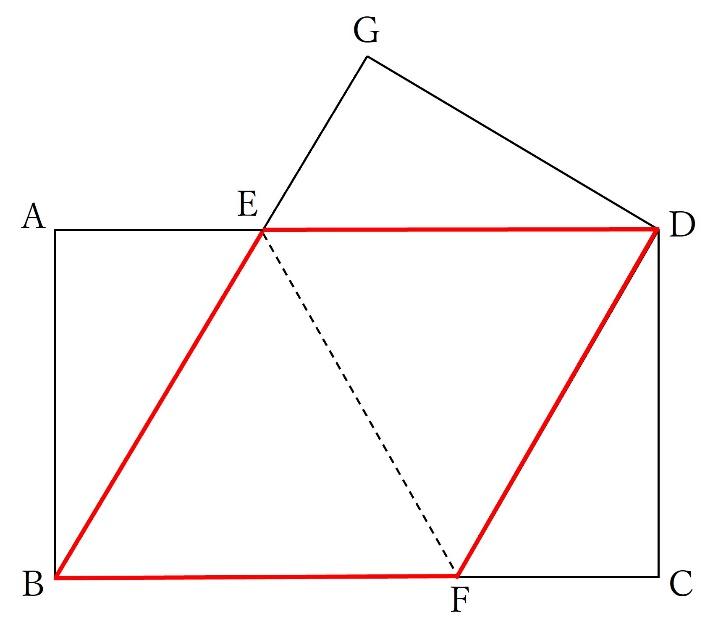
情報量が少なく、難易度のやや高い問題です。四角形EBFDは以下の赤線で囲まれた図形ですが、ひし形となっています。
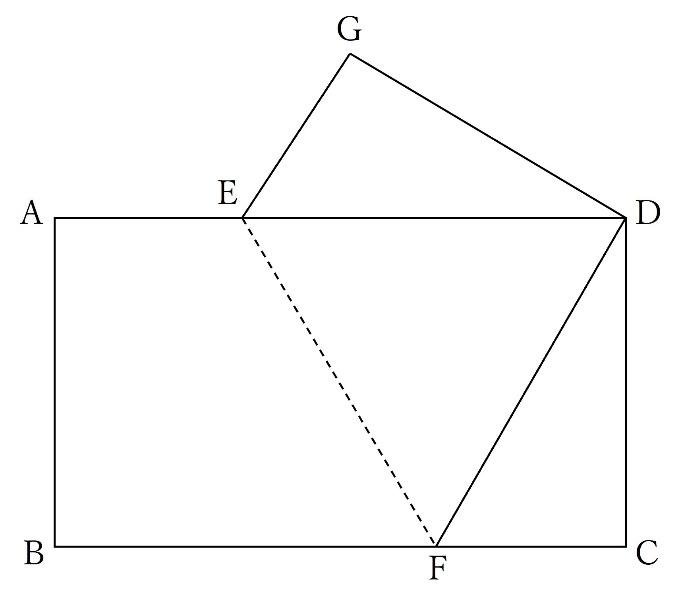
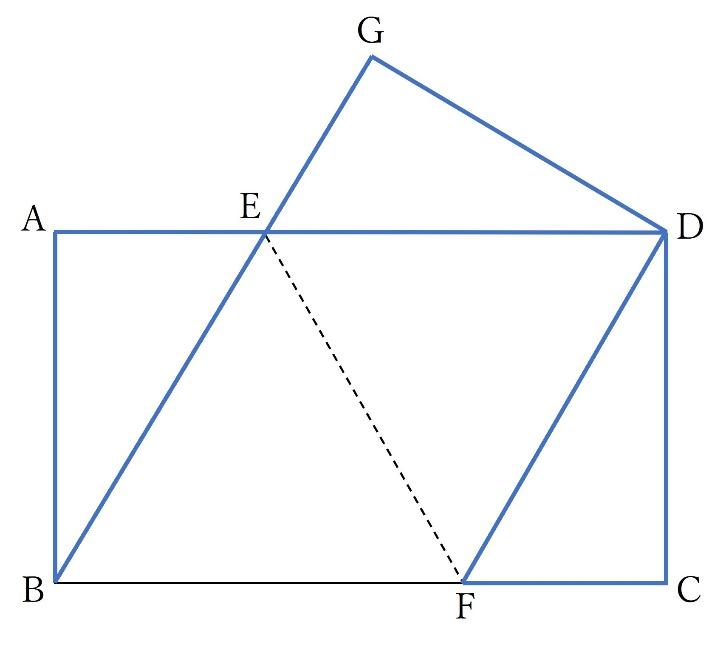
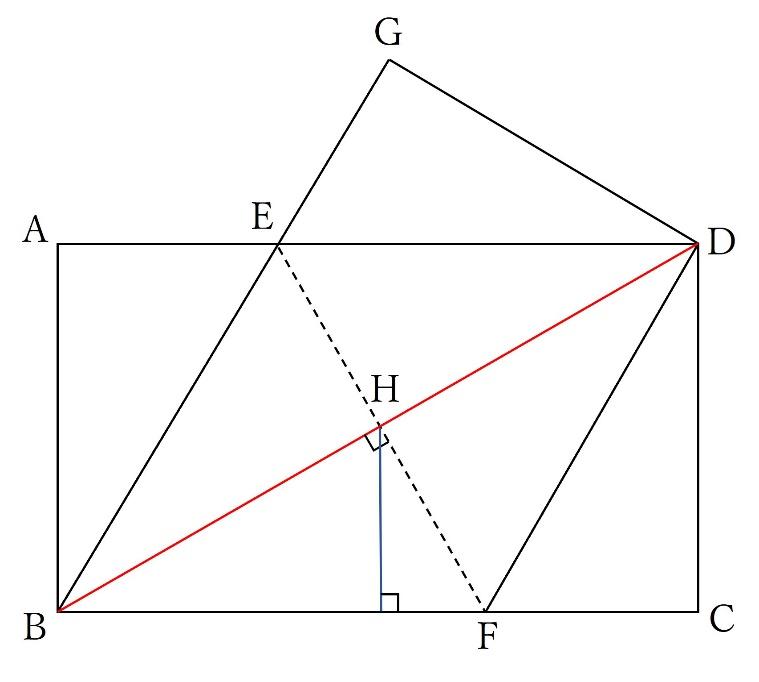
折り返しの角度が等しいことや、下の図の3つの青い三角形(三角形ABE、三角形GDE、三角形CDF)が合同であることに気付くことができれば、示すことは容易です。
さて、四角形EBFDはひし形だと判明したので、方針は立てやすくなりました。
(ⅰ) 対角線×対角線で面積を出す
(ⅱ) 平行四辺形のように底辺×高さで面積を出す
このそれぞれでアプローチしてみます。
(ⅰ)まずは対角線BDを引いてみます。
ひし形の対角線は垂直に交わります。
しかしこれ以上進めるのは難しいです。
BD・EFの長さを出すことができません。
(ⅱ)の方法で考えてみましょう。
(ⅱ)高さが12㎝と分かっているので、あとは底辺のBFを出すことが出来れば答えを出すことが出来ます。
ここで、自身が知っている図形を探すことが出来れば、以下の補助線を引くことが出来るはずです。図の青線です。
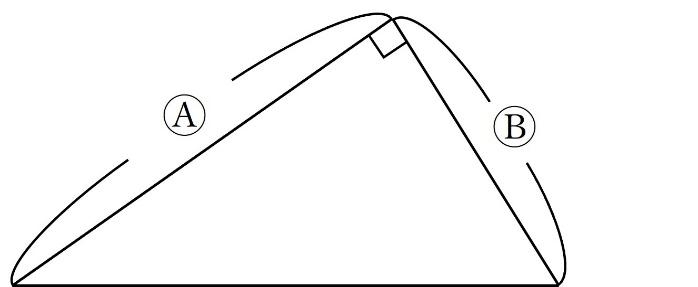
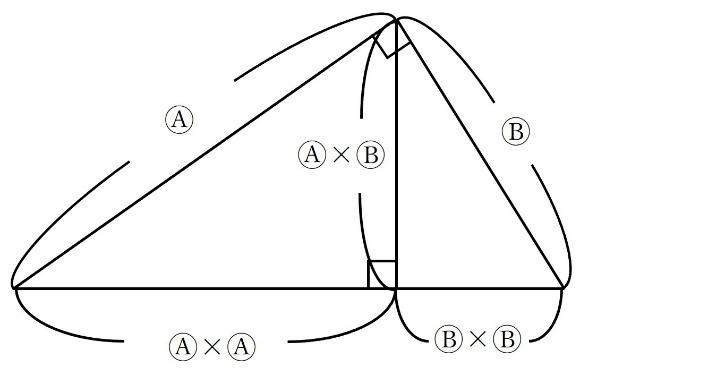
下の図のように、直角三角形の直角をはさむ2辺の比がわかっているとします。
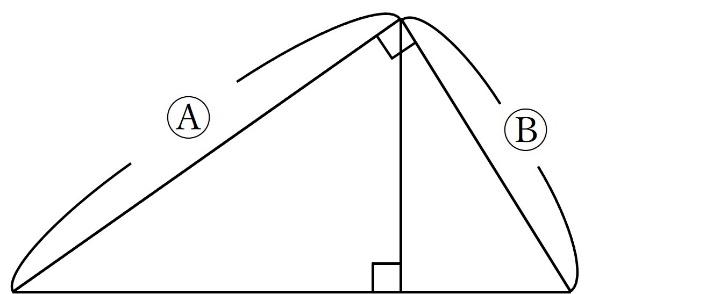
直角になっている頂点から斜辺に垂直に線を引きます。
このとき、直角三角形の辺の比は以下のようになります。
有名な分割ですので、知っている人が多いのではないかと思います。
さて、問題に戻りましょう。
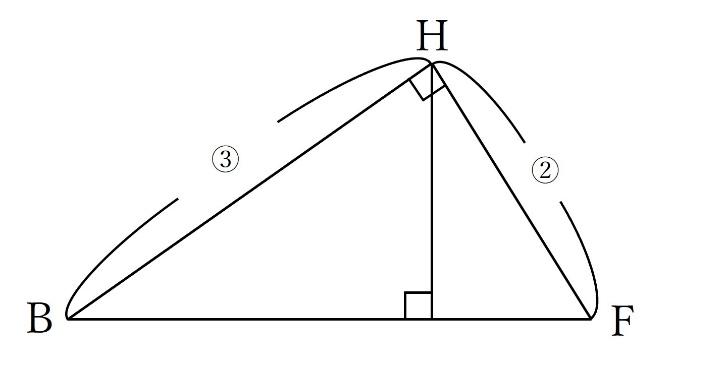
三角形HBFは三角形CBDと相似となります。よって、BH:HF=3:2となります。
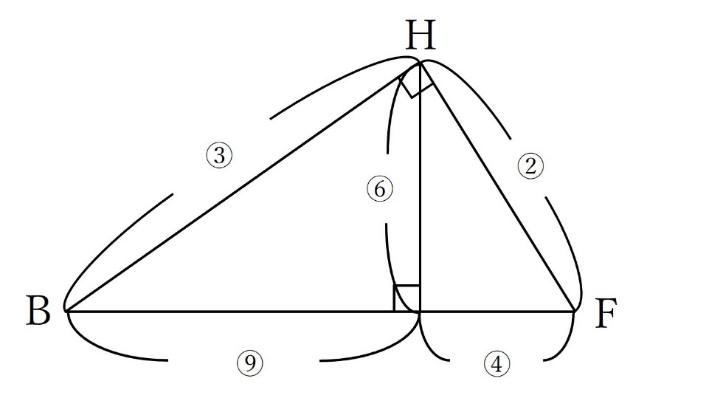
先ほどの分割を利用すると以下のようになります。
Hはひし形の対角線の交点ですので、中点となります。よって⑥=6㎝となり、⑬=13㎝
とわかります。
ひし形EBFDの面積は13×12=156㎠となります。
補助線を引くのに
-
図形の性質を活用する(ひし形の対角線)
-
自分の知っている形に持ち込む(直角三角形の分割)
という2つの考え方を使いました。
小6の子たちは過去問演習などで類似のトレーニングを行っていると思います。
非受験学年の子たちは図形の基本的な性質を学び、自分の知っている形をたくさん作っておくと、役立ちそうですね。
ご参考になれば幸いです。
それでは、今回はこれで失礼いたします。
受験Dr. 川上亮