みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。
今回もタイトルの通り補助線の引き方について、触れたいと思います。
今回お伝えしたいことは、補助線は「行き詰ったとき」に「自分の知っている形」に持ち込むために引くものだということです。
問題を紹介しつつ、解説していきます
まずは取り組みやすい問題からいきましょう。
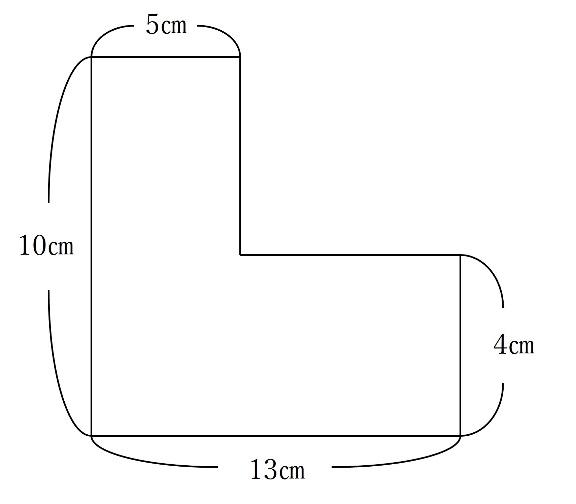
【問題】以下の図形は長方形を2つ組み合わせたものです。以下の図形の面積を求めなさい。
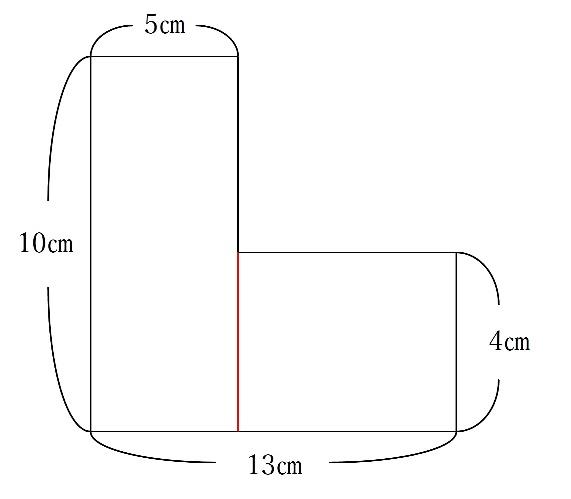
このままだと面積を出すことは出来ませんが、補助線を引き、長方形2つにわけることで面積を求めることが出来ます。
5×10+8×4=82㎠が答えとなります。
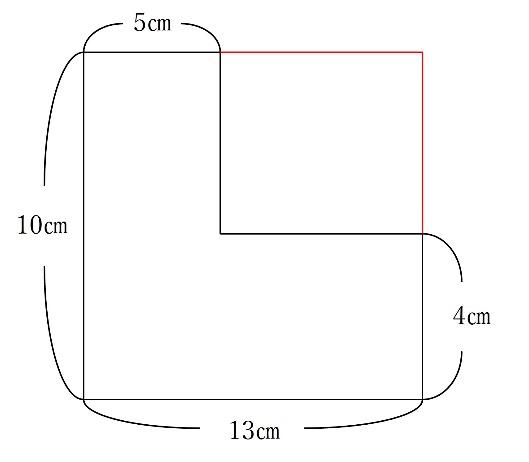
また、以下のように補助線を引くと、全体から右上の長方形を引くことでも答えを出すことが出来ます。
10×13-8×6=82㎠となります。
ポイントは、自分の知っている形に持ち込むということです。
それでは次の問題に進みます。
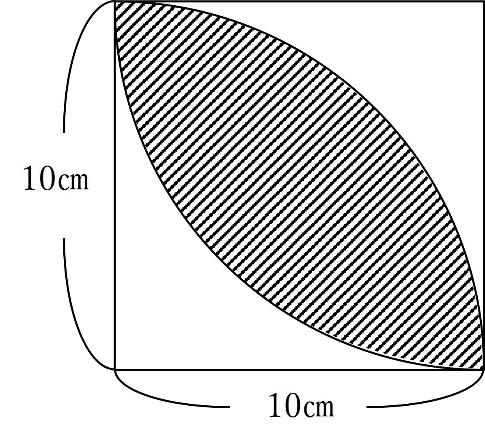
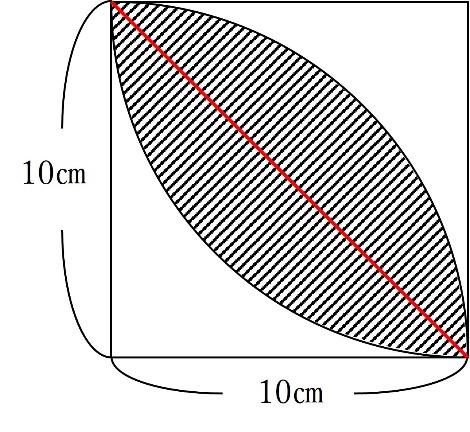
【問題】以下の斜線部分の面積を求めなさい。
有名な形なので、求め方を知っている子も多いと思います。
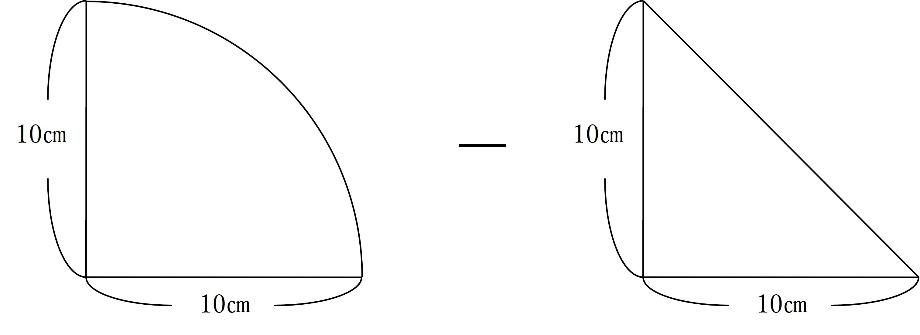
以下のように補助線を引くと2つの図形に分割できます。
赤線を引くことで、斜線部分は2つの図形に分かれます。それぞれ、半径10㎝の四分円から、直角二等辺三角形を引くことで求めることが出来ます。
(10×10×3.14×14-10×10×12 )×2=57㎠となります。
さて、それでは最後です。
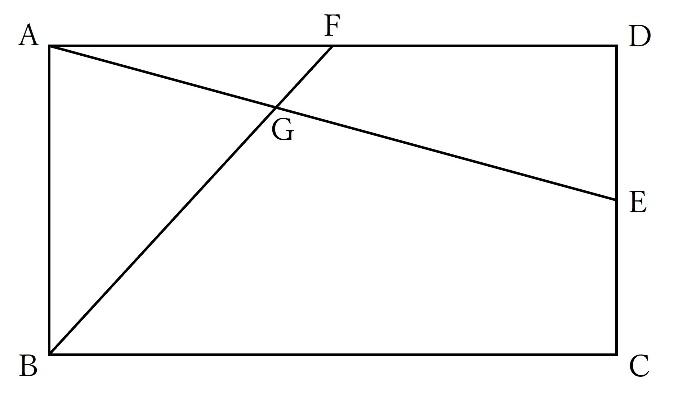
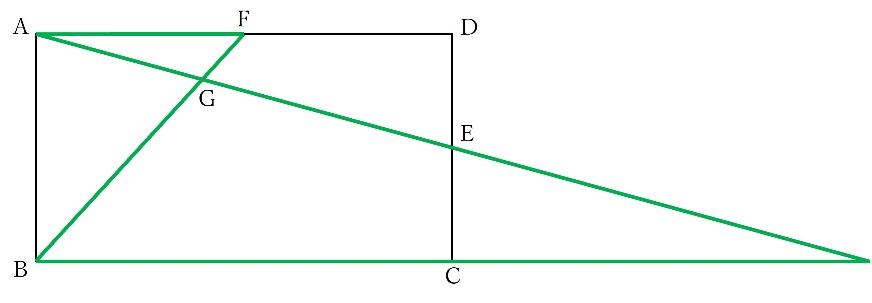
【問題】長方形ABCDは長方形で、点E・Fはそれぞれ辺の中点です。BFとAEの交点をGとします。このとき、次の問いに答えなさい。
-
AG:GEを求めなさい。
(2)BG:GFを求めなさい。
【解説】ここでは補助線の引き方だけ、触れていきます。
小5で学習する比の単元からの出題です。
平面図形と比では、相似という考え方を学習します。
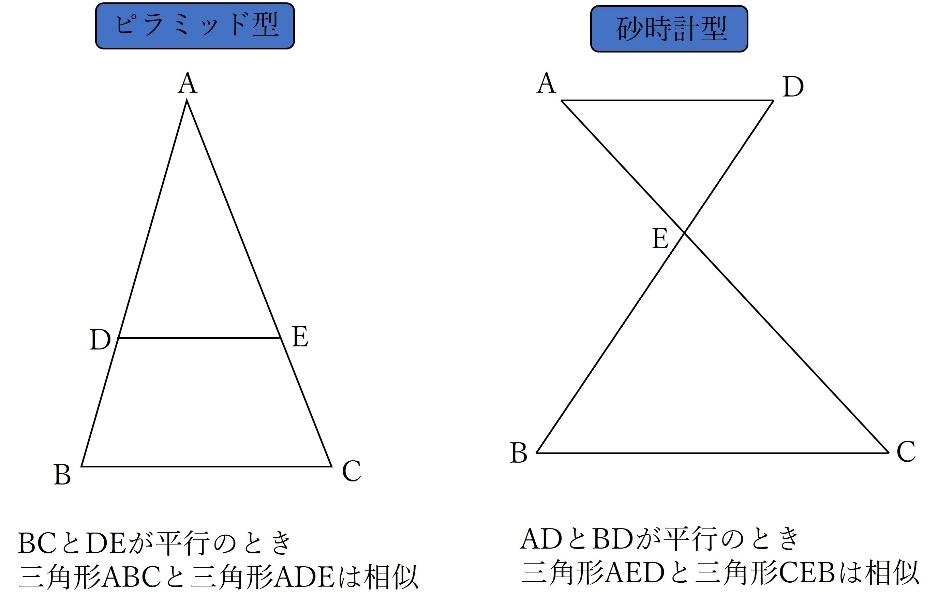
その中でも、ピラミッド型、砂時計型の相似はもっとも有名です。
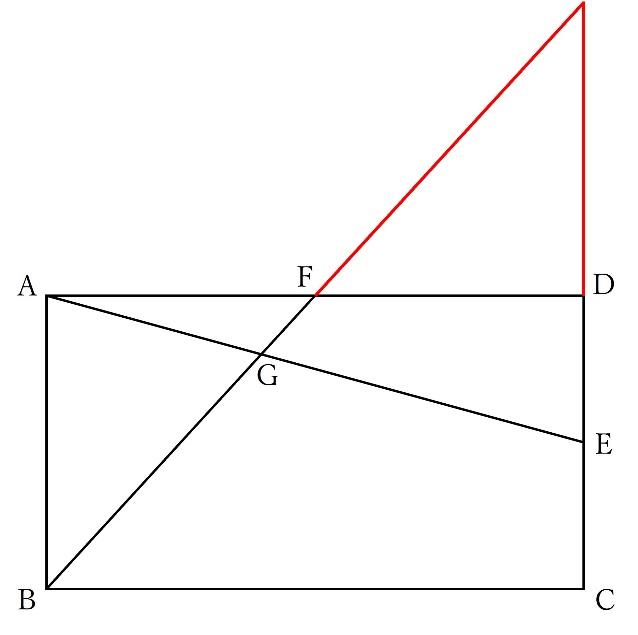
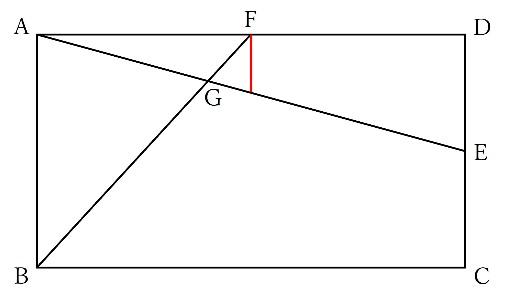
(1)問題の図の中にはこれらの相似型が見当たらないですが、以下のように補助線を引くことで相似な図形を作ることが出来ます。
図の赤線を引くことで、以下の砂時計型の相似が見えてきます。
この2つの三角形の大きさの比がそのままAG:GEとなります。
(この感覚が大切です)
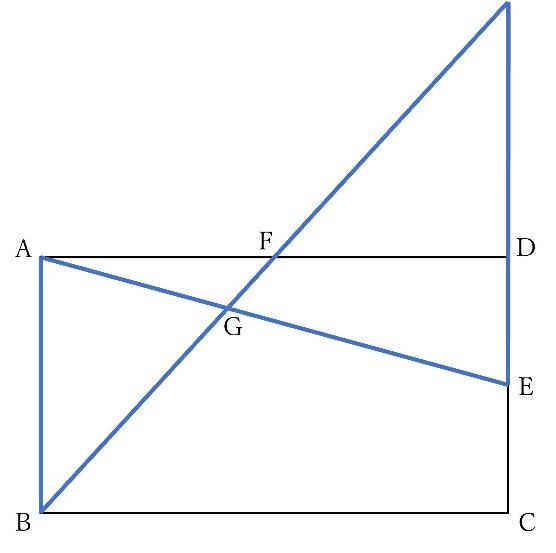
また、補助線を引いたことで以下の砂時計型の相似も見えてきます。
以上2つの砂時計型相似を使うと、答えは2:3となります。
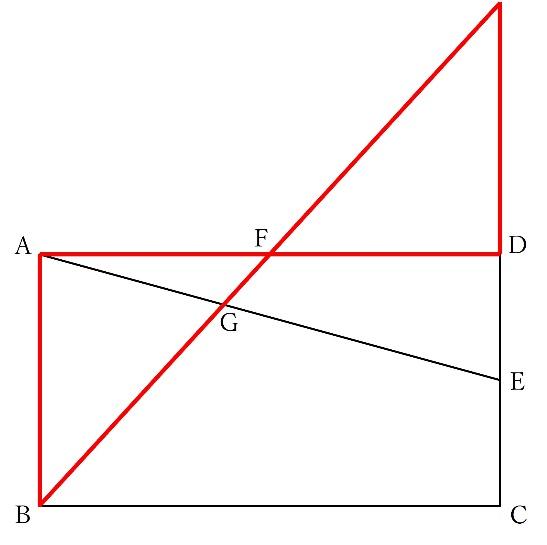
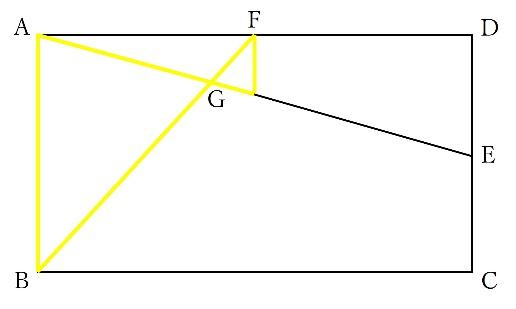
(2)(1)と同じように、三角形の大きさの比がBG:GFになるように補助線を引きたいところです。
以下の補助線が引けていればバッチリです。
以下の砂時計型相似を見据えています。
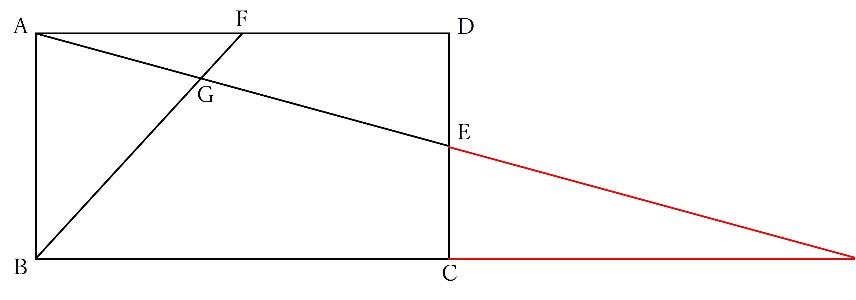
また、以下の補助線も考えられます。
以下の砂時計型を見据えています。
解答も念のため。4:1となります。
-
と(2)の違い、感じることが出来たでしょうか。
三角形の大きさの比がそのまま答えになるような補助線の引き方を心がけましょう。
いかがでしょうか。「自分の知っている形に持ち込む」という感覚を、少しでもご理解いただけると幸いです。
それでは、今回はこれで失礼します。
受験Dr. 川上亮