みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。
塾に通っている子たちは、新学年がスタートして1か月が経ちましたね。
そろそろ学習のリズムもつかめてきた頃でしょうか。
皆さんの頑張りを、心から応援しています。
我々講師陣は日々入試問題を解き、研鑽を積んでいます。私も沢山問題を解いていますが、今春の入試問題の中で印象に残った問題について、いくつか紹介できればと思います。
新小6の子たちにもチャレンジできる難易度の問題ですので、是非取り組んでみましょう!
それでは第一問です。注目するポイントによっては苦戦してしまうかもしれません。
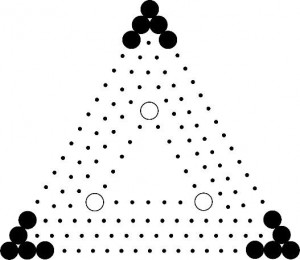
【問題】いくつかの白のご石を使って正三角形の形に並べたあと、さらに下の図のように585個の黒の碁石を、外側に3周囲むように並べ、正三角形の形を大きくしました。このとき、白のご石は何個並んでいますか。(東京都市大附属)
一番外側の白いご石が、1列に何個並んでいるかがわかればどうにかなりそうなのです。私ははじめ、全体から隅の黒いご石を引いて考えようとして失敗しました・・・(残った形が悪すぎました)
黒いご石の総数から、真ん中の列の黒いご石の数がわかるので、そこからアプローチすればすぐ答えが出ます。
一つの考え方に固執するのは良くないなぁと、改めて実感しました。行き詰まったときに、別の解法を考えようとする柔軟さはとても大切ですね。
さて、第2問です。これは意外と盲点となる単元かもしれません。
【問題】5点満点の算数のテストを10名の生徒が受けた結果の点数は次の通りです。
4,2,5,4,1,4,3,0,5,3
中央値の方が平均値よりも□点高いです。(世田谷学園)
データの活用からの出題です。中学入試で出題され始めて3年目になりますが、問題を見るとドキッとしてしまいます。
中学入試の算数といえば図形や整数問題、規則性などが王道ですし、その対策に時間を費やしてきた子がほとんどのはずですので、意外と手薄になりがちな単元です。
平均値は(合計得点)÷(人数)で求めることができます。
中央値・・・出せますか?この問題では3.5になります。(これから習う子も多いと思います)
多くの時間を費やす必要は無い単元だと思いますが、入試が近づいてきたら確認しておきましょう。
さて、最後の問題です。一見易しそうな取り組みやすい問題ですが、私と同じように固まってしまう子もいるかもしれません。
【問題】まっすぐな道路に地点Pと地点Qがあります。Aさんは地点Pを出発して地点Qに向かって歩き、地点Qに着くとすぐに折り返して地点Pに向かって歩きます。Aさんが地点Pを出発するのと同時にBさんは地点Qを出発して地点Pに向かって歩き始め、地点Pに着くとすぐに折り返して地点Qに向かって歩きます。AさんもBさんもそれぞれ常に一定の速さで歩きます。
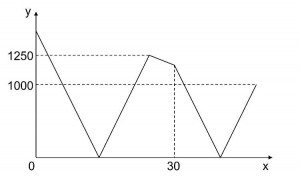
Aさんが地点Pを出発してx分後のAさんとBさんの距離をymとします。Aさんが地点Pを出発したのち再び地点Pにつくまでの間のxとyの関係は下のグラフのようになりました。このとき、地点PとQの距離を求めなさい。(灘 1日目 一部抜粋)
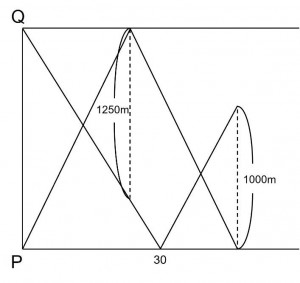
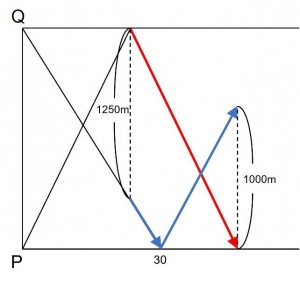
へだたりのグラフ、2者間グラフと呼ばれる問題です。グラフ自体は多くの子が見たことのあるものですし、一見簡単に解くことが出来そうです。私はダイヤグラムに書きなおすことが多いので、以下のように書きなおしました。
さて、ダイヤグラムに書きなおしたあと、私は数分固まりました(笑)
情報が少なすぎる気がして、本当に解けるのか疑問に思っていたのですが、ピンと閃きました(この瞬間が一番気持ちいいですね)。
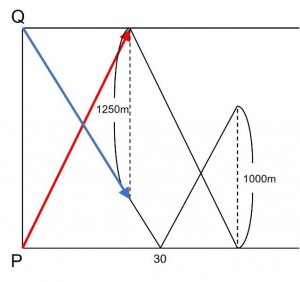
AさんがPQ間を進んだとき、Bさんは1250m進んでいます。(下の図の青線です)
ということはここも1250mになります。(下の図の青線です)
グラフの中の相似を使ったり、速さの比や時間の比について考えることの多い分野ですので、シンプルな考え方で攻略できるこの問題は強く印象に残っています。
いかがでしたでしょうか。
当然ですが、入試問題には中学入試を控える子たちに意識してほしい要素がたくさん詰まっています。だから我々は入試問題を解き、日々研鑽を積んでいるのです。
次回は今年の入試問題の中から、設定の練られた問題について紹介します。
それでは、今回はこれで失礼します。
受験Dr. 川上 亮