みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

本日はタイトルにもある通り、今春の入試問題の中から設定の練られた、状況整理の大切さがわかる問題を紹介致します。問題文が長いですが、是非頑張ってついてきてください。

 

問題

ある中学校の行事「A川歩行」ではA川に沿って数百人の生徒が一列になって一定の速さで歩きます。
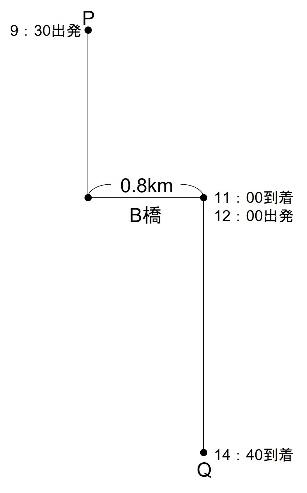
今年は川上の左岸のP地から、A川に垂直にかかった全長800mのB橋を一回だけ渡って、川下の右岸のQ地まで歩きます。
列の先頭はP地を午前9時30分に出発しました。
列の長さは、列の最後尾が歩きはじめるときに1.6kmになりました。
この列はB橋を渡り始めてから渡り終えるまでに30分かかり、列の先頭は午前11時ちょうどに渡り終えました。
B橋を渡り終えるとすぐに広い土手があって、着いた生徒から昼食休憩をとりました。
その後、正午にB橋を渡り終えた場所から再び列の先頭が出発し、時速3.6kmで歩きました。
このときも、列の長さは1.6kmになりました。
列の先頭がQ地に着いたのは午後2時40分でした。
また、ボートが午前8時55分にQ地を出発しました。
このボートは午前9時55分に生徒の先頭の列と出会いました。
A川の流れの速さを時速2kmとして、次の問いに答えなさい。【早稲田中　1回　一部抜粋】

（１）昼食休憩をとる前の生徒の列の速さは時速何kmでしたか。
（２）ボートの静水時の速さは時速何kmですか。

 

解説

各小問ごとに、必要な要素を抜き出して考えます。

 

（１）生徒の列には1.6kmの長さがあります。そして、全長800mの橋を列が渡るのに30分かかっています。そう、これは「通過算」の問題です。

(1.6＋0.8)÷＝時速4.8kmが答えとなります。

列車ではないので、通過算だと気付くことが出来なかった受験生もいたかもしれません。

 

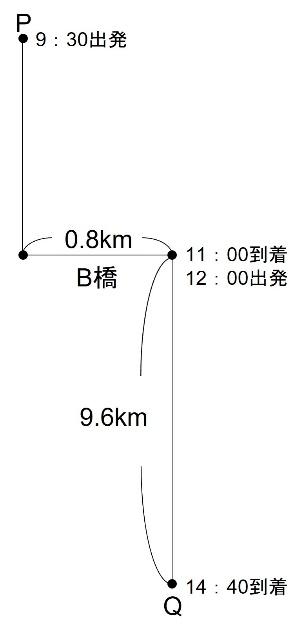
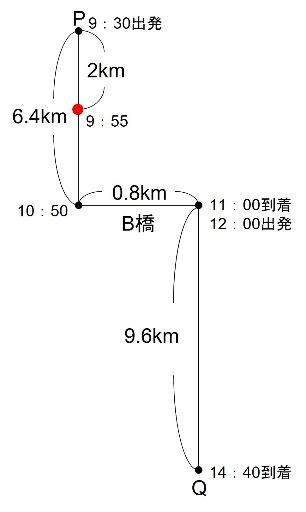
（２）です。まずは生徒の列について、わかっていることを図にまとめてみます。

 

 

生徒の列は休憩後、B橋を出発してからQ地まで時速3.6kmで2時間40分かかっています。よってB橋からQ地までの距離は
3.6×＝9.6kmとなります。

 

 

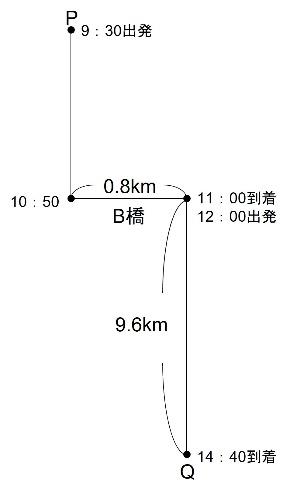
また、列の先頭は11：00にB橋を渡っていますが、このときの速さは時速4.8kmのため、B橋を渡るのに
0.8÷4.8＝時間＝10分かかっています。
よって、列の先頭がB橋を渡り始めたのは11:00の10分前ですので10:50です。

 

 

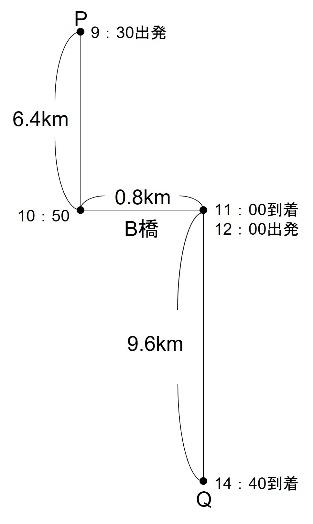
P地からB橋まで1時間20分かかっています。よって、P地からB橋までは
4.8×＝6.4kmとなります。

 

 

 

列の先頭は、9:55時点でP地から25分間進んでいます。よって、列の先頭はP地から
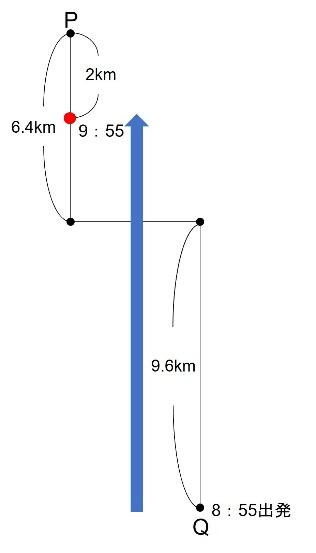
4.8×＝2km進んだところにいます。（下の図の赤点のところです）

 

 

 

よって、ボートは下の図の青い矢印の距離を、8:55～9：55の1時間で進むことになります。

 

 

 

(6.4＋9.6－2)÷1＝時速14km

これはボートの上りの速さになります。川の流れの速さは時速2kmですので、静水時の速さは
14＋2＝時速16kmとなります。

 

生徒の列に長さがあることや、B橋を渡る前後で速さが変わること、そして最後に流水算の要素があることなど、つまずきやすい要素がちりばめられており、非常に設定の練られた問題でした。典型題と呼べる問題ではないですが、いかに自分なりに情報を整理し、図にまとめるかが大切です。

1学期の間に速さを学習する際には、必ず線分図やダイヤグラムに情報をまとめてみてください。その積み重ねが、初見の問題でも必ず生きてきます。

それでは、今回はここまでにします。

受験Dr.　川上　亮