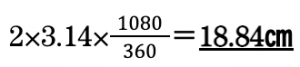みなさん、こんにちは。

受験Dr.算数・理科科の川上と申します。

 

前回の記事（2月9日）から間は空いてしまったのですが、補助線の引き方について触れていきます。

 

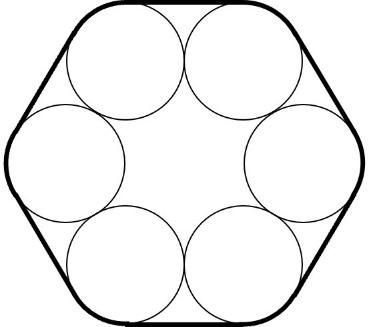
【問題】

 

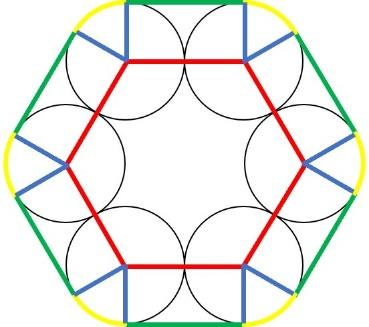
図のように、半径3㎝の円を6個並べました。この周りに図の太線のようにひもをぴんと張ってかけたとき、ひもの長さは何㎝になりますか。

 

 

さて、一見複雑な問題のように見えます。補助線を引くことで問題を解くことになるのですが、大前提として「自分の知っている形に持ち込む」ことが大切になります。

 

また、「どこからどこに引くか」についても、ある程度決まった方法があります。

慣れてくると、スラスラ補助線が引けるようになるかもしれませんね。

 

ポイント①　円の中心

 

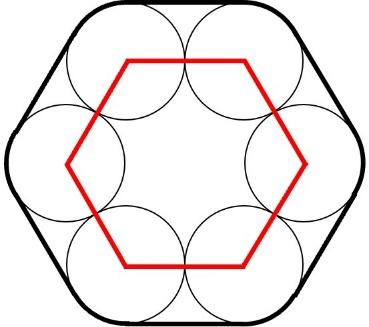
円の中心は、補助線を引く際には注目すべき点です。特に今回の図のように円が複数ある場合は、円の中心どうしを結ぶことが大きなヒントになることが多いです。今回は下の図の赤線のように中心どうしを結びます。

 

 

内側の赤い六角形が、1辺6㎝の正六角形になっていることも大切です。

 

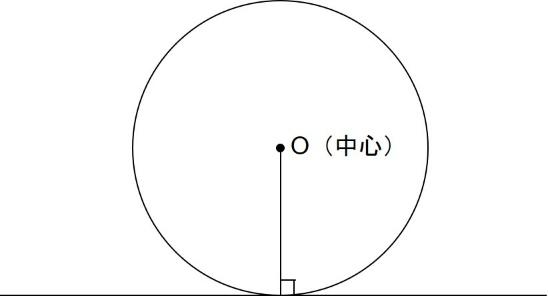
ポイント②　円と接線

 

上の図のように、円と直線が接している場合、下のように補助線を引くと垂直に交わります。

 

 

この引き方は知識として押さえておくと役に立つと思います。

 

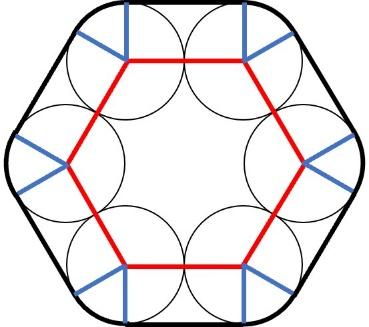
問題の図にも円との接点が多数あるので、青い線のように補助線を引いてみます。

 

 

ここまで引くと、問題の図の太線が直線部分と曲線部分に分かれていることに気付きます。（直線部分は緑、曲線部分は黄色にしてあります。）

 

 

直線部分の長さは内側の正六角形の周の長さと同じになっています。

また、曲線部分はおうぎ形の弧となっています。また、計算は割愛しますが中心角の和は360°です。

 

よって、6×6＋6×3.14＝54.84㎝となります。

 

さて、次は今春の入試問題にチャレンジします。

 

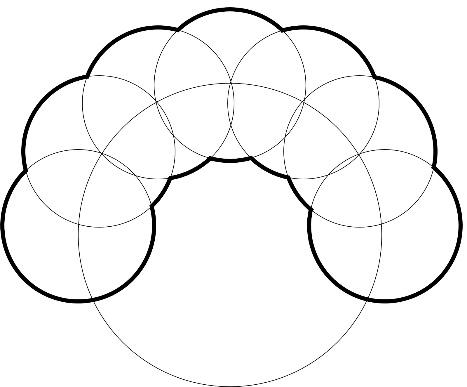
【問題】図のように、半径が2㎝の大きな円の周上に中心を持つ、半径が1㎝の小さな円が7つあります。また、小さな円の中心はその隣の小さな円の周上にあります。このとき、太線の長さを求めなさい。【2023　灘　1日目】

 

 

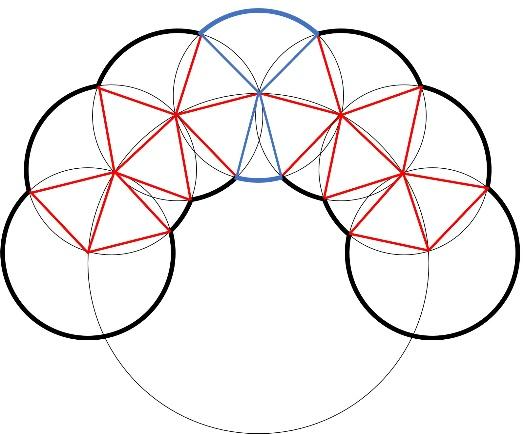
さっきの問題より、かなり複雑に見えますね。まずはポイント①に基づき、中心どうしを結んでみます。

 

 

さて、今回は接線が無いため、別の考え方が必要となります。

 

ポイント③　線と線の交点

 

ポイント②に通ずるところもありますが、線と線の交点も補助線を引く際に注意するポイントです。

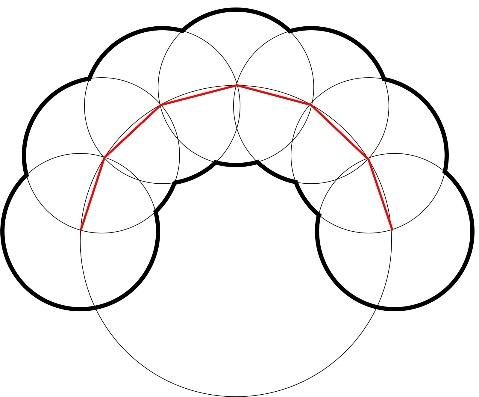
問題の図の小さい円の中心から、小さい円の交点に補助線を引いてみます。

 

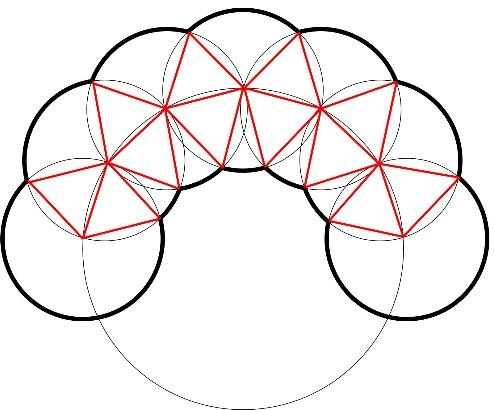
三角形がいくつも出来ました。もう気付いた子もいるかもしれませんね。この三角形は全て1辺1㎝の正三角形になっています。

 

さて、下の図の青いおうぎ形に注目してください。

 

 

正三角形の1つの内角が60度であることより、この2つのおうぎ形の中心角の和は120°となることがわかります。

 

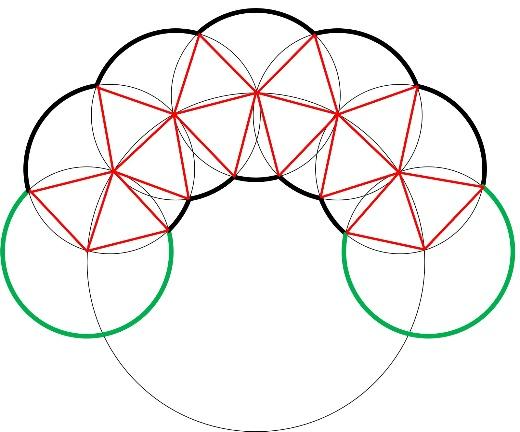
ちなみに、下の図の緑の部分は中心角が240°のおうぎ形の弧となっています。

 

 

中心角の合計は120×5＋240×2＝1080°

 

よって、となります。

 

大前提としての「自分の知っている形に持ち込む」という考え方、そして

 

ポイント①円の中心

ポイント②円と接線

ポイント③線と線の交点

 

1問目は①と②、2問目は①と③を組み合わせて解くことが出来ました。

 

いかがでしたでしょうか。

 

それでは、今回はこれで失礼します。

受験Dr.　川上亮