みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。
本日は、独断と偏見で、今春の入試問題の中から解けたときの爽快感が大きかった問題を紹介したいと思います。
まずは1問目!
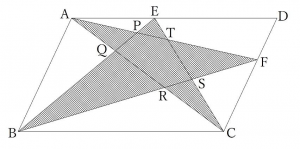
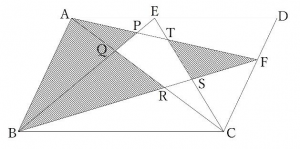
【問題】下の平行四辺形ABCDの面積が100㎠、五角形PQRSTの面積が9㎠のとき、図のかげをつけた部分(十角形AQBRCSFTEP)の面積を求めなさい。(洛星2023)
解けたときの爽快感を共有したいので、ぜひ挑戦してみてください。
下に解説を載せておきます。
【解説】
まず、明らかに情報が少ないです。全体の面積と、内部の五角形の面積の情報しかないため、この手の問題で多用する『相似』や『比』を利用する方法は除外した方がよさそうです。
また、求積の問題で使用する3つの考え方
1 分割する
2 全体から引く
3 移動させる
のうち、①は難しそう。ただでさえ☆型の十角形なので、分割してもいたずらに求めるところを増やすだけになりそうです。
②も×。引くところが多い。
よって③の、『移動させる』で行きます。移動させるためには、面積の等しいところを探さなければいけません。幸い、全体が平行四辺形なので、等積変形が使えそうです。
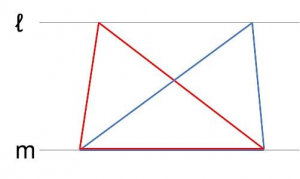
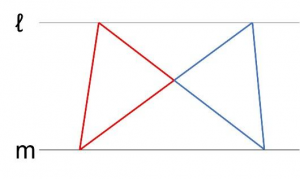
ℓとmが平行ならば、図の赤い三角形と青い三角形は面積が等しくなります。
また、共通部分をひくことで
この2つの三角形の面積も等しくなります。
さて、問題の図とにらめっこして・・・
上の図の赤い三角形の面積が等しいことがわかります。
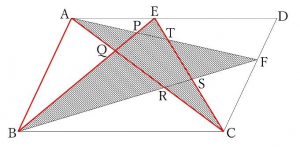
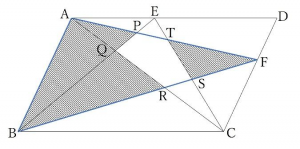
三角形EQCを三角形ABQに移動させてみます。
もう気付いた子もいるかもしれませんね。
上の図の青い三角形ABFは全体の面積の半分になっています。
よって、斜線部分の面積は100÷2-9=41㎠となります。
解法選択までの過程や、ダイナミックな結末が非常に印象に残る問題でした。
ちなみに、こんなにあっさり結論まで解説しましたが、実際に解いたときは結構苦戦したんです・・・だからこそ喜びが大きかったです(笑)
続いて2問目。
【問題】
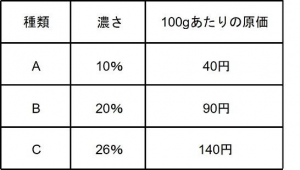
同じ物質が解けている水溶液がA、B、Cの3種類あります。それぞれの濃さと100gあたりの原価は下の表のようになっています。
ただし、水溶液の濃さとは、水溶液の重さに対する解けている物質の重さの割合のことです。
これらをいくらかずつ混ぜ合わせることで、別の濃さの水溶液を作ります。例えば、例えば、Aを300g、Bを200g混ぜ合わせると、14%の濃さの水溶液が500gできます。この500gの水溶液を作るには300円かかるので、できる水溶液の100gあたりの原価は60円となります。
(1)AとCを混ぜ合わせて、100gあたりの原価が110円の水溶液を作ります。AとCの重さの比はどのようにすればよいですか。最も簡単な整数の比で答えなさい。また、出来る水溶液の濃さを求めなさい。
(2) BとCを混ぜ合わせて、100gあたりの原価が110円の水溶液を作ります。BとCの重さの比はどのようにすればよいですか。最も簡単な整数の比で答えなさい。また、出来る水溶液の濃さを求めなさい。
(3) AとBとCを混ぜ合わせて、100gあたりの原価が110円で、濃さが22%の水溶液を作ります。AとBとCの重さの比はどのようにすればよいですか。最も簡単な整数の比で答えなさい。
(2023 麻布)
濃度に関する問題です。問題の難度はそこまで高くありませんが、(3)を解いたときの優越感が記憶に残っています。
下に解説を載せておきます。
【解説】
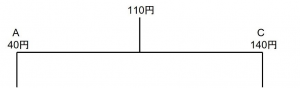
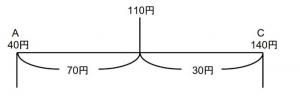
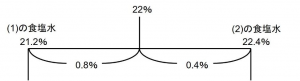
濃度の問題なので、以下のようにてんびん図にまとめてみます。
支点からの距離が以下のようになります。
あとは逆比を利用して
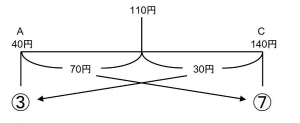
より、A:C=3:7となります。また、このときの濃度を求めます。AとCを3:7で混ぜ合わせるので
今度は重さの比がわかっているため、支点からの距離の比が求まります。
比の10にあたる量が26-10=16にあたるため、比の1にあたる量は16÷10=1.6です。
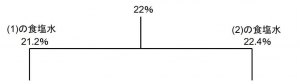
これを利用して、濃さは21.2%となります。
も全く同じ解法になります。B:C=3:2、濃さは22.4%となります。
(3)3つを混ぜる、そして原価と濃さも指定されているので難しそうな問題ですね。
さて、私はとにかく算数の問題を解くときには楽をしたい!面倒くさいのは嫌だ!効率良く問題を解くことを意識しています。
はじめ、(3)を解くにあたり、表を見返して、濃さと原価について改めて整理して・・・と、思っていたのですが、あることに気が付きました。
『(1)も(2)も(3)も原価が110円になっている』
そこでひらめきました。
『(1)と(2)の答えで出た食塩水を混ぜてしまおう』
原価が110円どうしの水溶液をどんな割合で混ぜ合わせても原価は110円のままですよね。
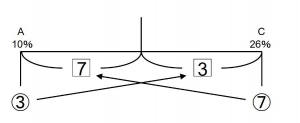
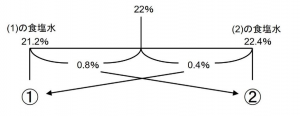
というわけで、以下のようにてんびん図にまとめました。
支点からの距離がわかります。
逆比を利用して
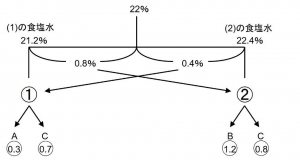
(1)の水溶液はAとCが3:7の割合で含まれており、(2)の水溶液はBとCが3:2の割合で含まれています。よって
上の図のようにA、B、Cに分けました。それぞれ
A=0.3
B=1.2
C=0.7+0.8=1.5
よって0.3:1.2:1.5=1:4:5が答えとなります。
(3)の解法に気付いたのがもしかして自分だけなのではないかと、優越感に浸ることができた問題でした(笑)
いかがでしたでしょうか。
問題を解けたときの爽快感、優越感は算数を好きになる要素のひとつだと思います。
少しでも感じ取っていただければ幸いです。
それでは、今回はこれで失礼します。
受験Dr. 川上亮