みなさん、こんにちは。

受験Dr.算数・理科科の川上と申します。

 

今回も前回に引き続き、補助線の引き方に触れていきます。

やや難しい内容ですが、是非最後までお付き合いください。

 

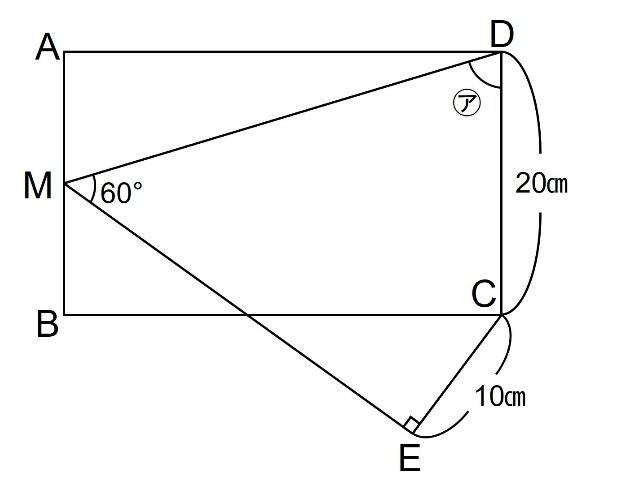
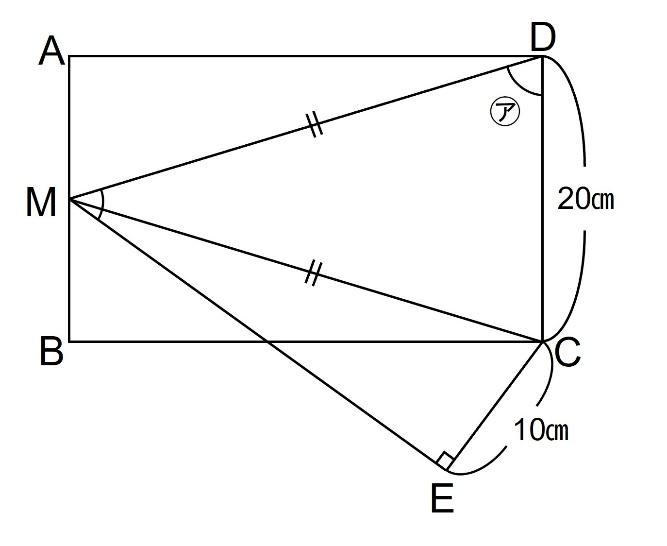
【問題】下の図で、四角形ABCDは長方形で、辺ABの真ん中の点がMです。また、2本の直線CE、MEは垂直です。このとき、角㋐の大きさを求めなさい。【2018　灘　1日目】

 

 

一見、すんなり求まりそうな問題ですが、そう簡単ではありません。

私も見た目の取り組みやすそうな印象にだまされました・・・

（美味しそうなものを食べたら全然思っていた味と違った、みたいな・・・伝わりますか？）

 

さて、ヒントも少ないため、補助線を引いてみましょう。

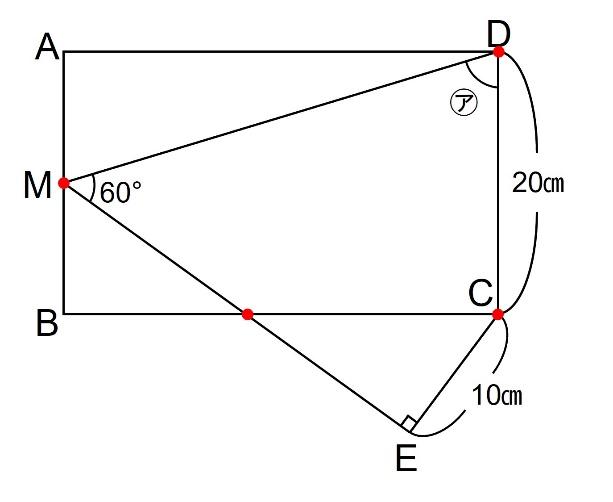
前回の内容の復習ですが、線と線の交点は補助線を引く候補となります。

 

 

交点となっているところはこれだけあります。（図の赤点です）

 

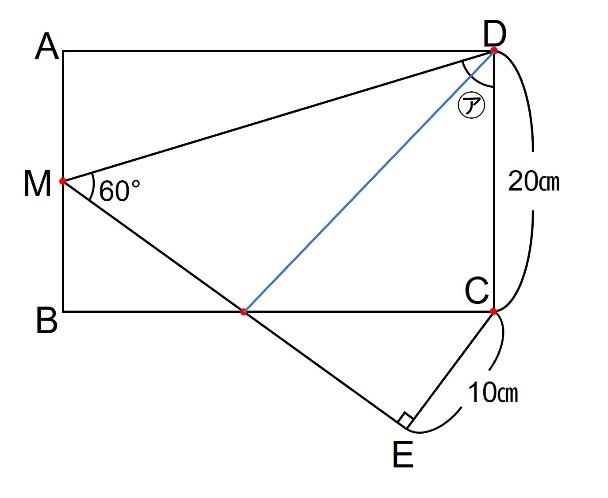
赤点どうしを結ぶことを考えると、実は補助線は以下の2種類の候補しかありません。

 

もう一つは

 

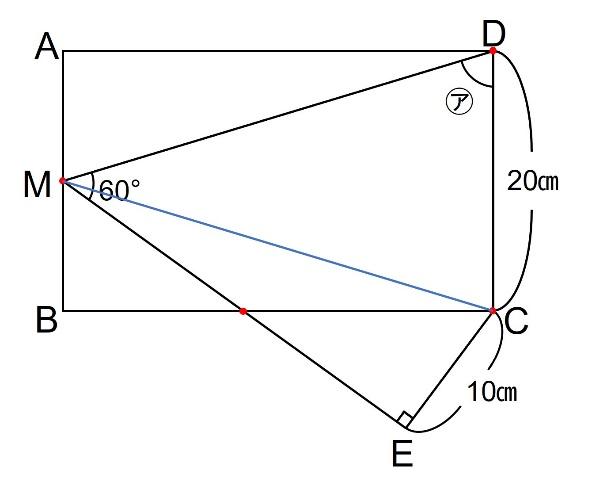
です。MCに補助線を引いた図において、Mは中点ですので、三角形DMCは二等辺三角形です。

 

 

ここで、補助線を引くポイントについて触れたいと思います。

 

ポイント①　合同な図形を作る

ポイント②　二等辺三角形の性質を利用する

 

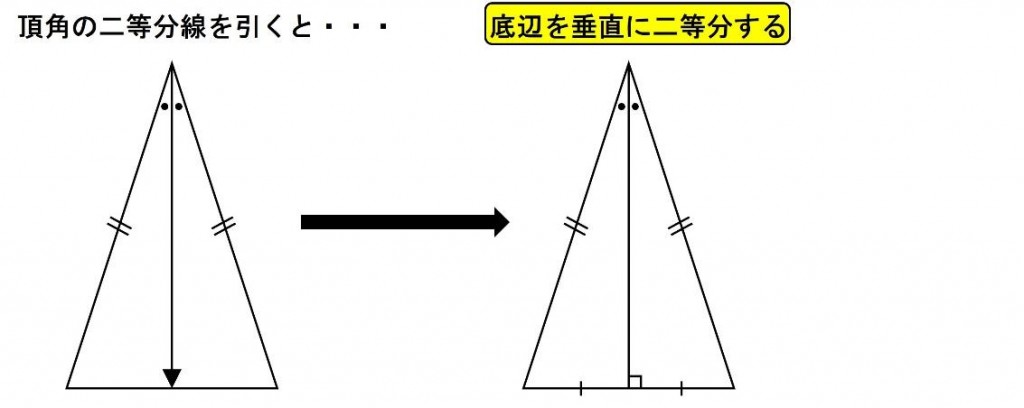
二等辺三角形は、頂角から角の二等分線を引くと、底辺を垂直に二等分する性質があります。

 

 

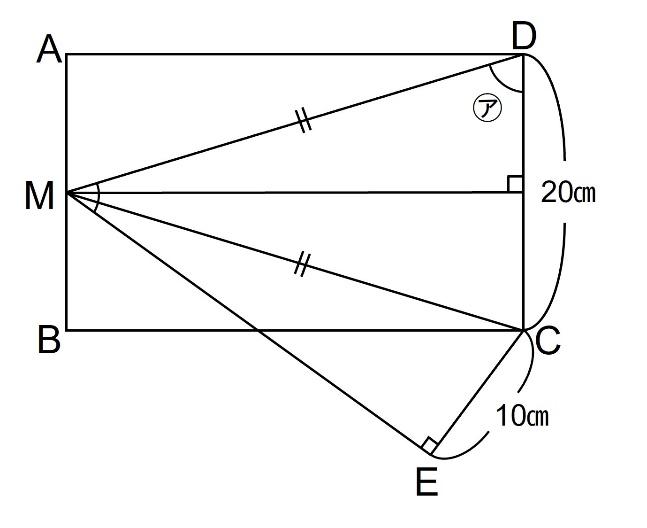
MからDCに向かって角の二等分線を引くと以下のようになります。

 

さて、ここで気付くと気持ちいいですよ？少し考えてみましょう。

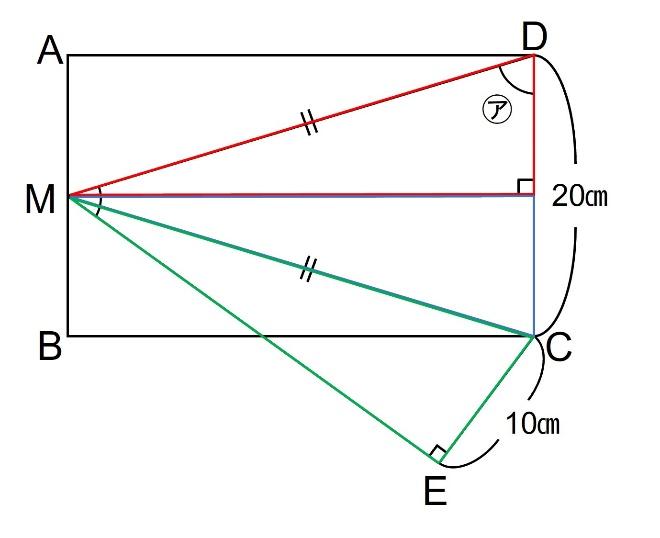
下の3つの三角形（赤、青、緑）が合同となっています。（DC＝20㎝、CE＝10㎝という条件がここで活きています）

 

これを利用し、㋐＝70°となります。

 

続けてもう一題です。

 

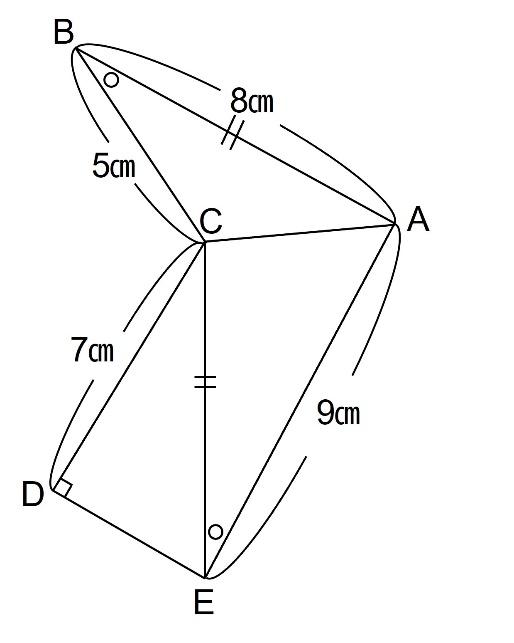
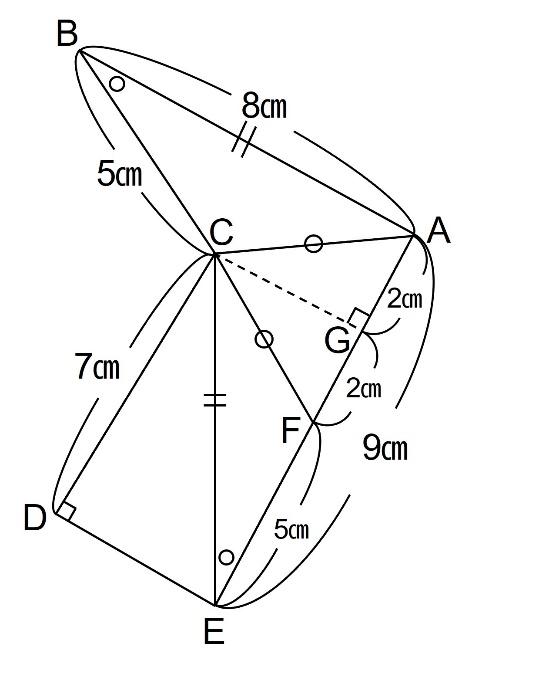
【問題】下の図において、AB、CEの長さはどちらも8㎝で、印〇をつけた角の大きさは等しいです。このとき、四角形ACDEの面積は三角形ABCの面積の□倍です。【2020　灘　1日目】

 

ちなみこの問題は見た目の通り、難しいです！（笑）

 

さて、どこから手をつけるべきかが難しい問題ですが、先ほどのポイント①　合同な図形を作る　より、以下の補助線を引くことが出来ると、正答にぐっと近づきます。

 

 

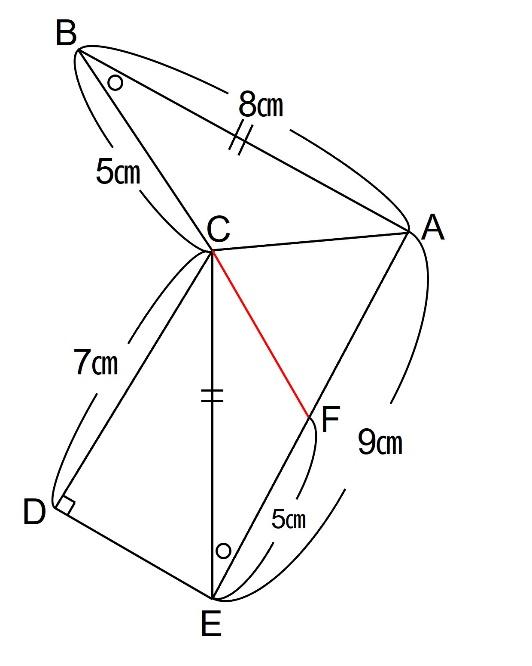
EF＝5㎝となるようにFをとり、CFを結ぶことで三角形CEFと三角形ABCが合同となります。

 

 

また、三角形CEFと三角形ABCが合同ですので、三角形CFAはCF＝CAの二等辺三角形となります。

 

 

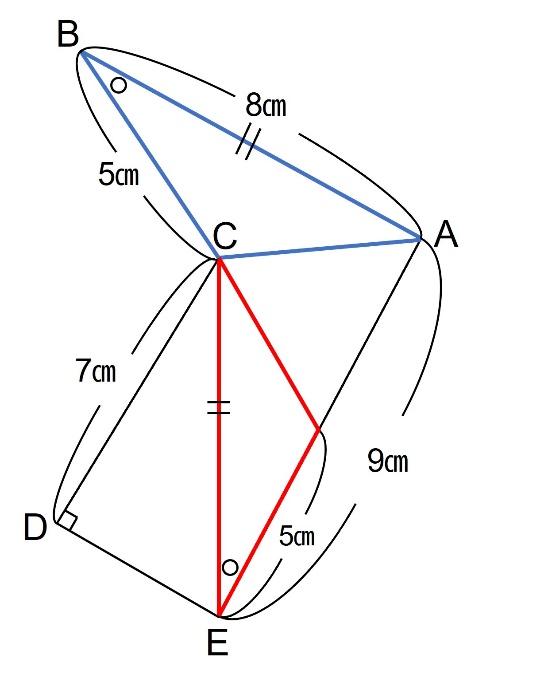
二等辺三角形が見つかったということは、ここでポイント②ですね。二等辺三角形の性質を利用します。

 

上の点線のように補助線を引くと、底辺が垂直に二等分されます。

 

FG＝2㎝なので、EG＝7㎝となります。

 

さあ、あと一息です。

 

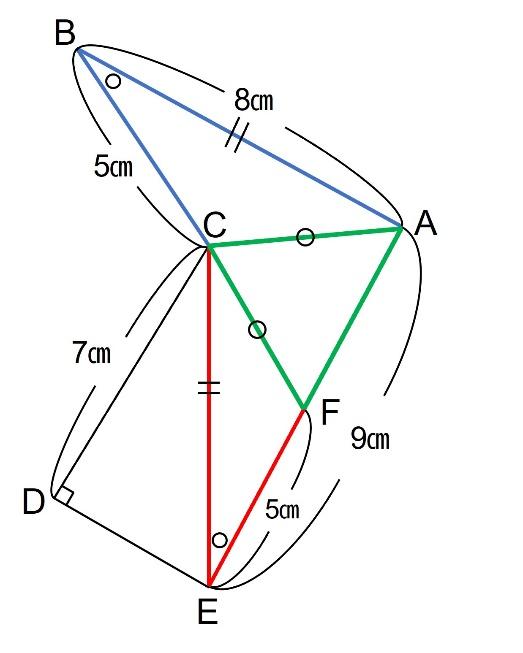
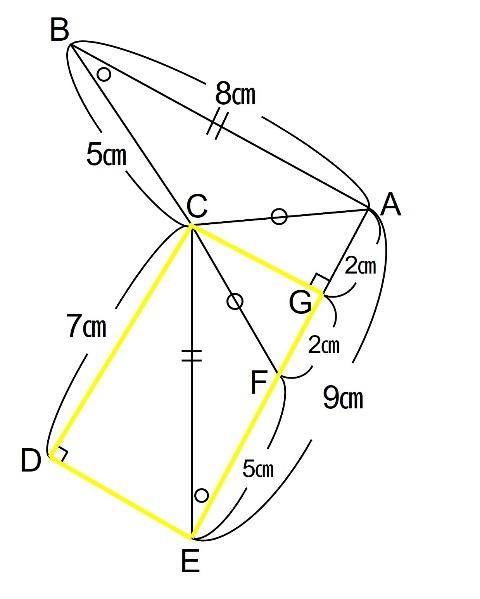
三角形CDEと三角形EGCが合同になることを利用すると、四角形CDEGは長方形となります。

 

 

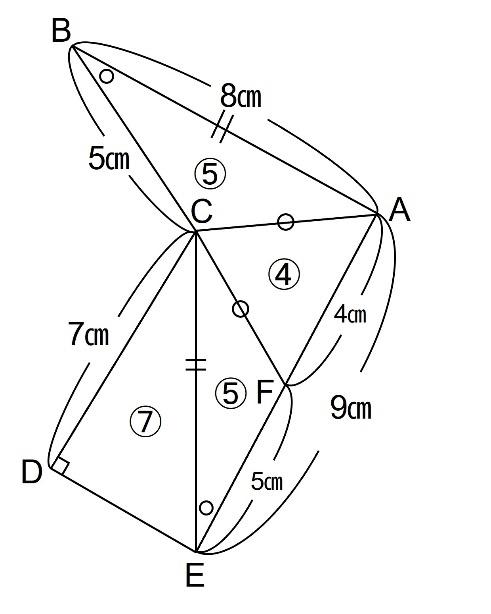
DE＝CGより、三角形CDEと三角形CEFと三角形CFAの面積比は底辺の比と等しく、7：5：4となります。また三角形CEFと三角形ABCが合同であることを利用すると下の図のようになります。

 

 

四角形ACDEの面積は4＋5＋7＝16より、16÷5＝3.2倍となります。

 

ポイント①　合同な図形を作る

ポイント②　二等辺三角形の性質を利用する

 

どちらの問題もポイントを押さえていたとしても難しい問題でしたね。

最後までお付き合いいただきありがとうございました。

 

それでは、今回はこれで失礼します。

 受験Dr.　川上亮