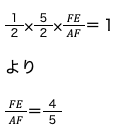みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

今回は辺の比を求める問題について触れたいと思います。

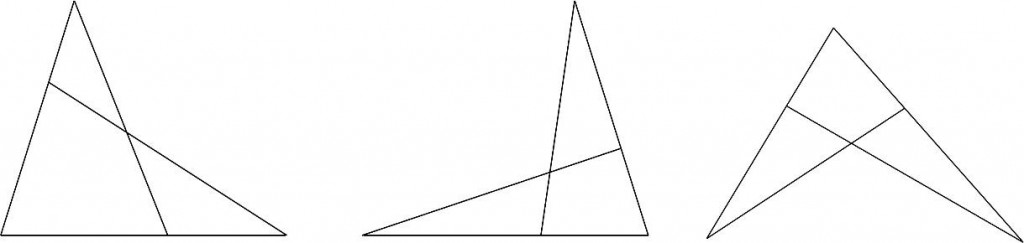
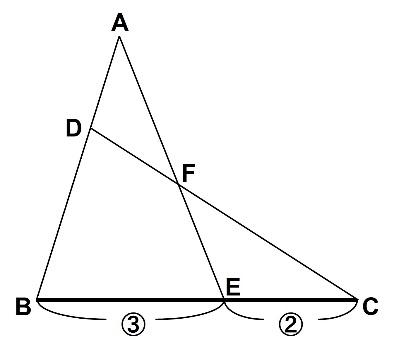
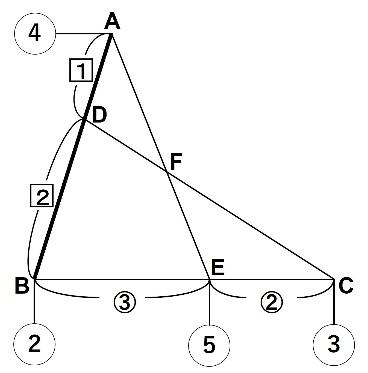
以下の図をご覧ください。

 

どれも2つの三角形が、ひとつの角を共有して重なっています。
私は「キツネ」っぽいなぁ・・・と勝手に思っています。

 

 

さて、この形を題材にした問題で有名なものに、辺の比を求めるものがあります。

解法が複数あり、学習塾によって、そして指導する先生によって好みがあると思います。
我々個別指導の講師は、様々な状況、環境の子たちを指導します。
そのため、複数の解法を知っておかなければなりません。

今回は代表的なものをいくつか紹介します。

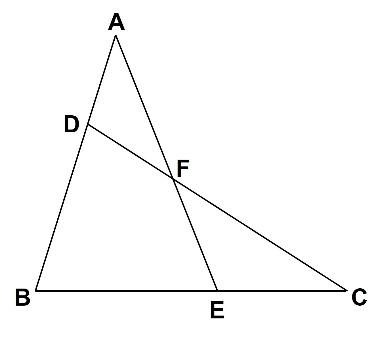
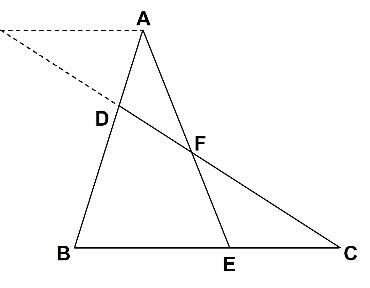
以下の問題をご覧ください。

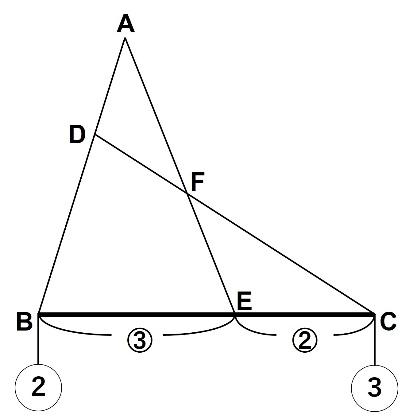
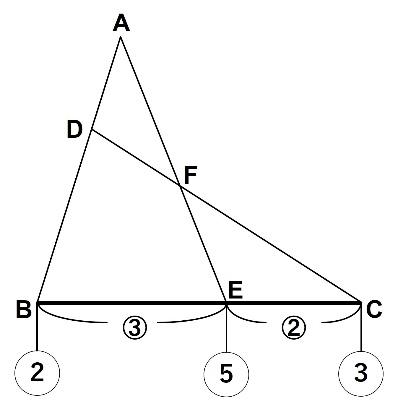
【問題】AD：DB＝1：2、BE：EC＝3：2のときAF：FEを求めなさい。

 

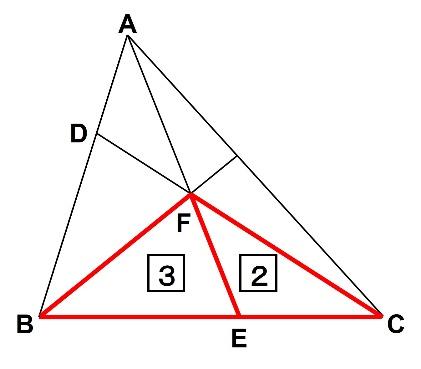
解法①　ベンツ切り

最も有名な解法かもしれません。面積比を利用する方法です。
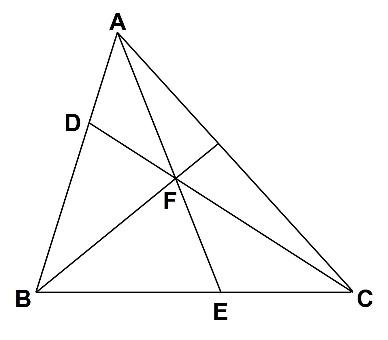
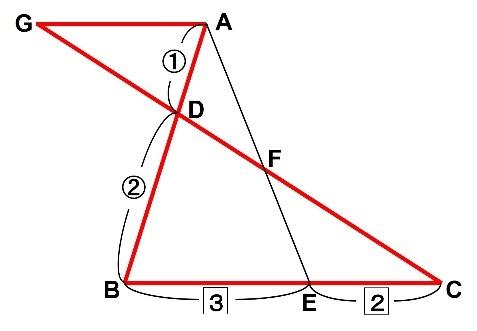
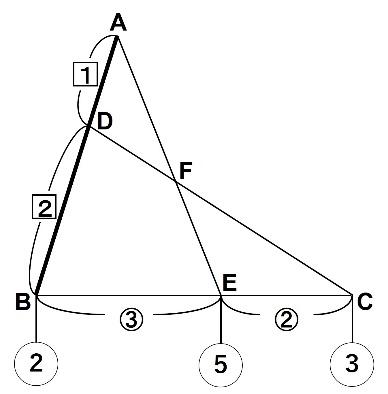
以下の図のように、ACを結び、BFを延長します。

 

 

三角形FBEと三角形FECの面積の比はBEとECの長さの比に等しくなり、3：2となります。

 

 

また、三角形AFCと三角形FBCの面積の比はADとDBの長さの比に等しくなります。三角形FBCは5なので、三角形AFCの面積はその半分の2.5です。

 

 

三角形AFCの面積と三角形FECの面積の比が2.5：2＝5：4となるため、AF：FE＝5：4となります。

ベンツ切りは知っている子が多いと思います。面積比がサクサク出てくる感覚が気持ちいですよね。

 

さて、2つ目にいきましょう。

 

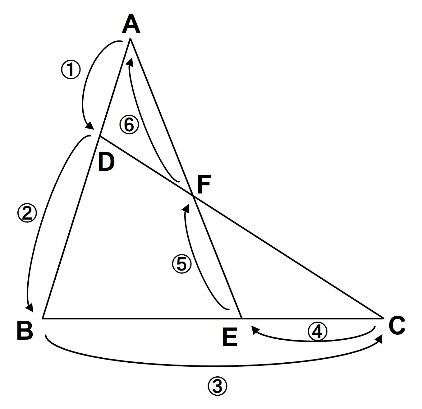
解法②　メネラウスの定理

これも有名な解法です。使いこなすことができれば強力な武器になります。

 

 

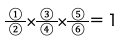
～⑥の値を

に当てはめると、解答が導き出せるというものです。
道順の設定や、1回寄り道しなければならないことなど、慣れるまで時間はかかりそうですが、習得するとスピーディーに解くことができます。

今回の問題だと

となります。よって、AF：FE＝5：4です。

メネラウスの定理は、証明を中学校で学習するため、使用を控える塾や先生も多いように思いますが、使いこなすことができればなかなかの破壊力。中学入学以降は使用率もグンと上がります。

 

３つ目に行きましょう。

 

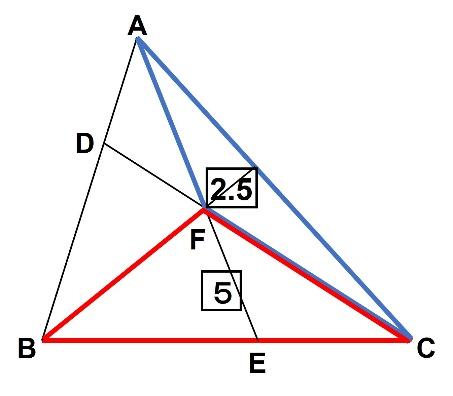
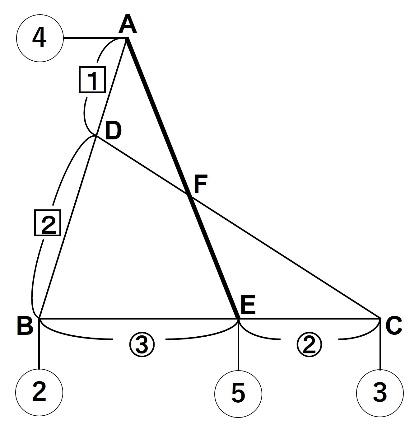
解法③　補助線の活用

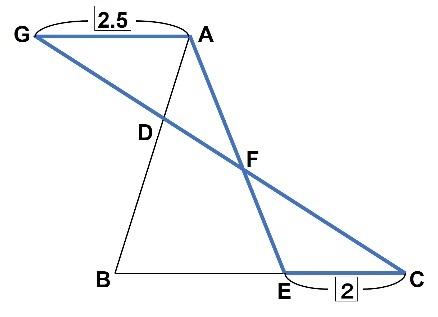
補助線を引き、砂時計型の相似を利用する方法です。

 

 

解法①と同じく、スイスイ解ける感覚があり、私は一番好きかもしれません。

 

 

赤い砂時計に注目するとGAが2.5とわかります。そして

 

 

図の青の砂時計に注目します。AF：FE＝2.5：2＝5：4です。

①、②と比べても、基本的な相似を2回使用すれば終わるこの爽快感が最高です。

 

さて、最後の解法です。

 

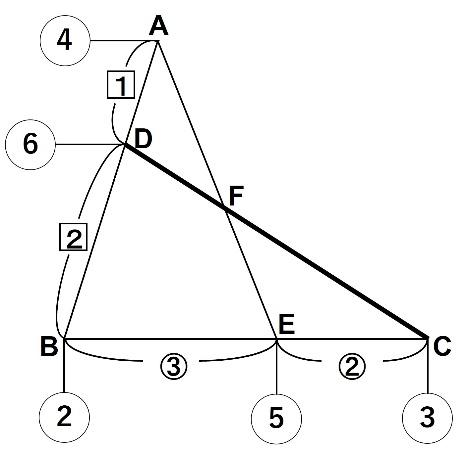
解法④　てんびんの利用

理科で「回転力＝支点からの距離×力」

という式を用いて計算する問題を一度は解いたことのある子がほとんどでしょう。

この図形の中の辺をてんびんに見立てて計算する、というなんとも不思議な解法です。

まずBCを、Eを支点とするてんびんと見なします。

 

BE：EC＝3：2より、てんびんをつりあわせるためには、BとCにはそれぞれ重さの比が2：3のおもりをつるす必要があります。

 

支点にはあわせて5の力がかかります。

 

 

続けてABを、Dを支点とするてんびんと見なします。

 

 

AD：DB＝1：2であること、そしてすでにBに重さ2のおもりがつり下がっていることより、Aには2×2÷1＝4のおもりをつるす必要があります。

 

 

最後にAEを、Fを支点とするてんびんと見なします。

 

 

Aには4のおもり、Eには5のおもりがつり下がっているので、AF：FE＝5：4となります。

「なにこれ？」というのが初めて見たときの感想でした。今も「なにこれ？」と思っています（笑）

正直個人的にはあまり好きな解法ではないのですが、進めていくうちに他の辺の比もついでに出せるので、すごく便利なんです・・・

今回の例だと、Aの④のおもり、Bには②のおもりがつり下がっているので、Dには⑥の力がかかります。

DCに注目すると・・・

 

 

DF：FC＝3：6＝1：2となります。

今回の問題とは直接関係ないですが、例えば連番で

(1)AF：FEを求めなさい
(2)DF：FCを求めなさい。

という出題形式であればとても便利ですね。

「これなら使えそう！」と思ってもらえる解法が1つでもあれば幸いです。

それでは今回はこれで失礼します。

受験Dr.　川上亮