みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

今回は正多面体の中の正多面体について触れていきます。

「なにそれ？」という子もいるでしょうから、まずは例を挙げてみます。

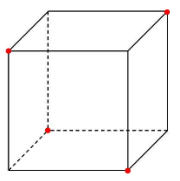
上の立方体の色を付けた点を結んでみると・・・

全ての面が合同な正三角形の「正四面体」が現れます。

（ちなみにこの正四面体と、立方体の体積比は出題されることが多いです。
この正四面体は、立方体から三角すいを4つ引くことで作られています。
この三角すいの体積が立方体のだとすぐわかれば1：3とわかるはずです）

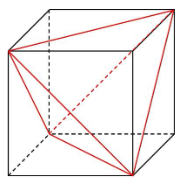
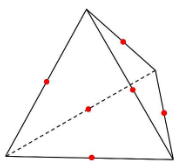
さらに、下の立方体をご覧ください。

今度は各面の対角線の交点（図の赤点）を結んでみます。すると・・・

「正八面体」と呼ばれる立体が現れます。
（ちなみに、この正八面体の体積は立方体の体積のです。
正八面体を正四角すい2個とみなすと、底面は立方体の、高さは立方体と等しいためです。）

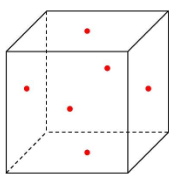
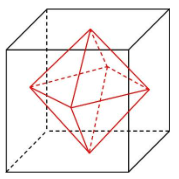
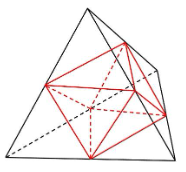
さらに、下の図をご覧ください。

全ての面が正三角形の正四面体（先ほど立方体の中に出てきました）です。

各辺の中点（図の赤点）を結ぶと・・・

やや見づらいですがまたまた正八面体が出てきます。

もしかしたら、ここまでの流れで「当たり前じゃん」と思ってくれる子もいるかもしれませんね。

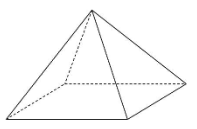
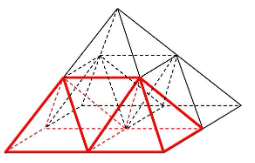
さて、最後にマニアックなものも紹介します。もとの立体が正四角すいのため、正多面体ではないですが、内部に多面体が隠れています。

辺の長さがすべて等しい正四角すいです。

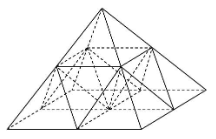
各辺の中点をとり、以下の図のように分割します。

かなりごちゃごちゃしていますが、正四角すい6つと正四面体4つに分割されています。
（これはかなり見づらいかもしれません・・・頑張ってください！）

次の図の方が見やすいかもしれません。

正四角すい2つと正四面体1つを赤色にしています。どうでしょうか。

ただ、入試で見ることが少ないため、記憶の片隅にずっとしまっていたら・・・

 

【問題】

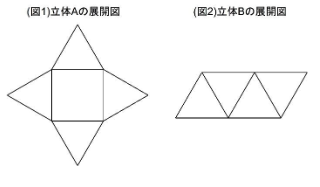
図1のような、すべての辺が3㎝の正方形1つと正三角形4つでできた展開図があり、そこからできる立体Aがあります。また、(図2)のようなすべての辺が3㎝の正三角形4つでできた展開図があり、そこからできる立体Bがあります。

(1)(2)省略

(3)立体Aを2つと立体Bを1つ使って、それらをくっつけて立体Dを作ります。ただし、立体と立体をくっつけるときは、正三角形どうし、または正方形どうしの面をぴったりと重ねることとします。考えられる立体Dの中で最も面の数が少ない立体の展開図をかきなさい。【渋谷幕張中　2023　一部抜粋】

 

で、出た！
まさにさっきの赤線で囲った立体です。

我々講師側は、妥協せずすべてを担当生徒に伝えて入試に送り出さないといけないのだと痛感しました。

今回の内容で、役に立つものが一つでもあれば幸いです。

 

それでは今回はこれで失礼します。

受験Dr.　川上亮