みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

今回は回転体について触れていきます。

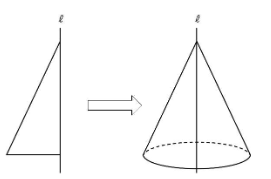
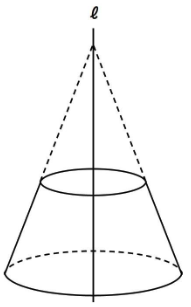
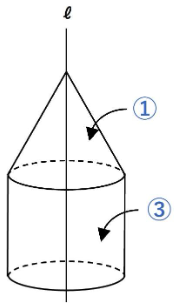
下の図のような三角形をℓを軸に回転すると円すいに

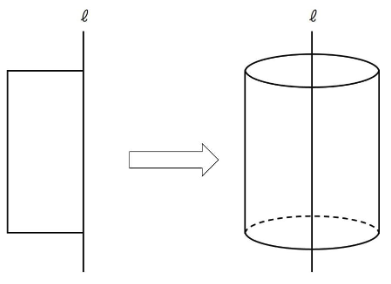
長方形を回転させると円柱になります。

見たことのある人も多いのではないでしょうか。
慶應中等部のように出題頻度の高い学校もいくつかあり、押さえておきたいテーマの一つです。（慶應中等部の回転体は表面積を求めるケースがほとんどですが）

 

今回は体積を求めるために、体積比を活用する考え方を紹介します。

 

（問題①）

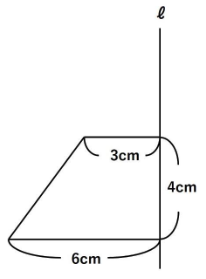
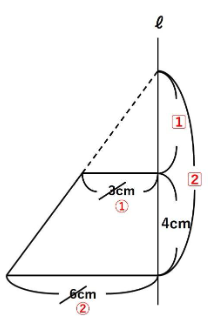
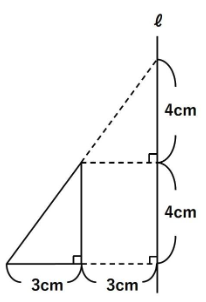
下の台形を、ℓを軸に1回転したときにできる立体の体積を求めなさい。

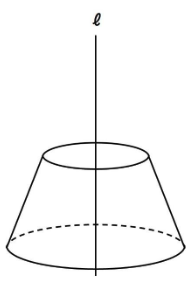
慣れないうちは見取り図を描きましょう。以下のような円すい台になります。

角出しすると、解法が見えてくるのではないでしょうか。

相似を利用して、小さい円すい（見取り図の上の円すい）の高さを出しておきましょう。

相似比は3：6＝1：2ですので、高さは4㎝となります。

大きな円すいから小さな円すいを引けば答えが出そうですね。

となります。

計算量が多く、めんどくさい・・・じゃなくて、もう少し楽をしたいですね。
相似比と体積比の関係を利用してみましょう。

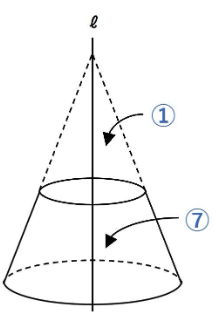
小さな円すいと大きな円すいは相似比が1：2です。相似比が1：2ということは、体積比は1×1×1：2×2×2＝1：8となります。

小さな円すいの体積を①とおくと、円すい台の体積は⑧－①＝⑦となります。

だいぶスッキリしましたね。

 

さて、次に進みます。

 

（問題②）

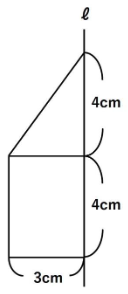
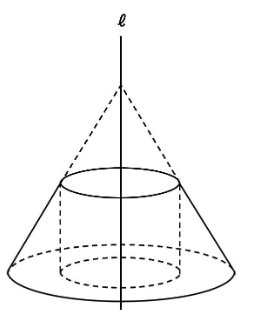
下の図のような長方形と直角三角形を、ℓを軸に1回転させてできる立体の体積を求めなさい。

見取り図は以下のような、円柱と円すいを組み合わせた形になります。

円すいと円柱の体積をそれぞれ求めて足しても答えは出ますが、体積比を使いましょう。
図の円すいと円柱は、底面積、高さともに等しくなっています。

円すいと円柱の体積の公式を思い出してください。

違いは「」です。

よって、図の円すいと円柱の体積比は1：3となります。

円すいの体積は

全体の体積はこの4倍なので

12×4×3.14＝48×3.14＝150.72㎤となります。

 

さて、少し難しくします。

 

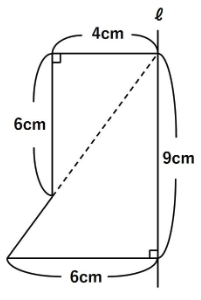
（問題③）

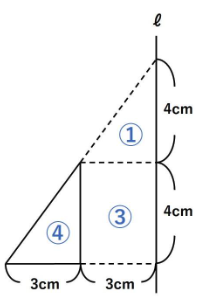
以下の図をℓを軸に1回転させてできる立体の体積を求めなさい。

さて、今回の見取り図は以下のようになります。

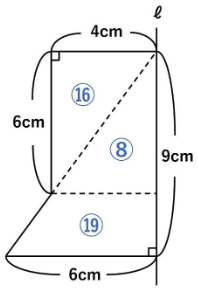
大きな円すいから、小さな円すいと円柱を引いても出そうですが、めんどくさい計算が煩雑になりそうなので今回も体積比でいきましょう。

今回は回転させる前の図に体積比を書き込んでいきますよ～！

せいっ↓↓↓↓↓

※問題①で使用した相似比→体積比と、問題②で使用した底面積と高さが等しい円柱・円すいの体積比を組み合わせて考えています。

 

最後は難しいかもしれません。

 

（問題④）

以下の図をℓを軸に1回転させてできる立体の体積を求めなさい。

円柱と円すい台の体積をそれぞれ出して・・・ではなく、体積比でいきますよ。

ほれっ↓↓↓↓↓

上の図のようになっていればパーフェクト。

よって

 

回転体の求積は、体積比を活用することでめんどくさい計算を少し省略することができ、慣れるととても便利です。ぜひ練習してみてください。

今回の内容がひとつでもお役に立てば幸いです。

それではこれで失礼します。

受験Dr.　川上亮