みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

今回は前回に引き続き回転体について触れていきます。

難易度高めの題材にしましたので頑張ってついてきてください！

それではいきましょう。

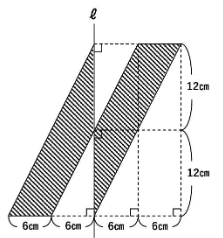
(問題１)図の斜線部分を直線ℓの周りに1回転させてできる立体の体積を求めなさい。【2015　洛星】

見るからに複雑そうな形をしていますね。
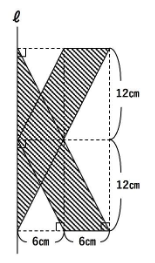
まず、左右非対称な形の回転体の問題では、片方を折り返して考えます。

さて、この図形を回転させるわけですが、見取り図を・・・書く気になれません（涙）

解法はさておき、この図のまま処理する子が多いのではないでしょうか。
パップス・ギュルダンを使用する方法もありますが、前回の体積比を使って攻略していきましょう。

全体をいきなり考えるのは大変なので、一部を抜き出して考えます。
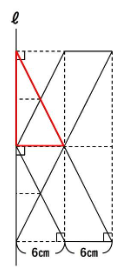
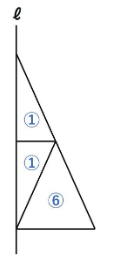
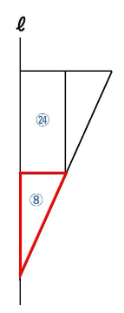
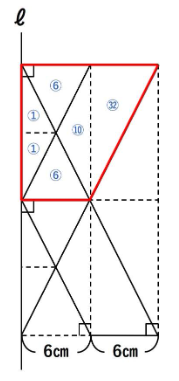
まずは下の図の赤い三角形からいきましょう！

この三角形はピラミッド型の相似になっており、相似比は１：２です。

相似比が１：２ということは、体積比は１×１×１：２×２×２＝１：８でしたね。
同じ円すいのことも考慮すると下の図のような体積比になります。

まだまだ先は長いですが、元気よく行きましょう！
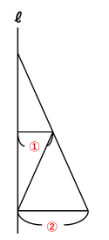
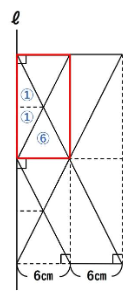
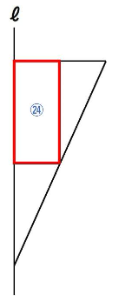
次は下の長方形を抜き出して考えます。

底面積と高さが同じ円すいと円柱の体積比は１：３でしたね。
円すい部分が①＋①＋⑥＝⑧ですので、円柱の体積は㉔となります。
同じ体積の部分を考慮し、以下のようになります。

少しずつ埋まってきましたね！パズルのように、数値を埋めていくこの感覚、癖になってきませんか？（笑）
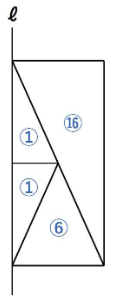
さて、また少し範囲を広げて抜き出します。以下の部分です。

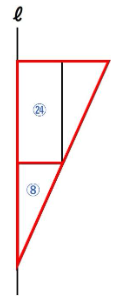
円柱部分（下の図の赤線で囲った部分）はまとめて①＋①＋⑥＋⑥＋⑩＝㉔となります。また、下の図の三角形の相似を利用します。

くり返しになりますが、底面積と高さが同じ円すいと円柱の体積比は１：３です。

円柱の下の円すいは㉔÷３＝⑧となります。

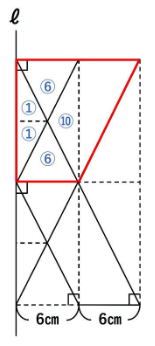
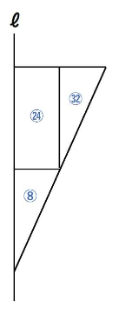
さて、残りは円柱の右の部分ですね。

下の図のピラミッド型の相似を利用します。

相似比は１：２ですので、体積比は１×１×１：２×２×２＝１：８です。
小さい円すいの体積が⑧ですので、大きい円すいの体積はその８倍です。円柱部分を考慮すると以下のようになります。

終わりが見えてきました！

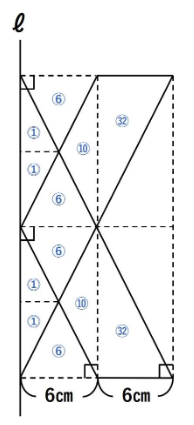
今まで求めた体積比をまとめると以下のようになります。

図形の対称性を利用すると

上の図のようになります。求める体積は①のちょうど100倍になりますので

３×３×3.14×６××100
＝1800×3.14
＝5652㎤

となります。

ひとつひとつ順を追って説明すると長く感じますが、慣れると驚くほど短時間で解けるようになります。

ミス無く、正確に数値を求めるトレーニングを積めば、体積比を使用する解法は非常に強力な武器となります。解法の難度が高く、習得するまでが大変ですが、最難関校を目指すのであれば、ぜひとも練習してみてください。

今回の内容がひとつでもお役に立てば幸いです。

それではこれで失礼します。

受験Dr.　川上亮