みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

今回はタイトルにもある通り、場合の数について扱っていきます。

皆さんは、場合の数好きですか？
私は全ての単元の中で、一番嫌いです！（特に、難しい問題だと手間はかかるし、当たり前ですけど1つ漏れがあるだけで不正解だし・・・）

今回の内容を通して、基本的な考え方を参考にしていただければ幸いです。

まずは問題です。

 

問題1

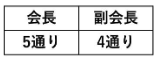
(1)5人の生徒の中から、生徒会の会長と副会長を決める方法は何通りありますか。
(2)5人の生徒の中から2人の掃除当番を決める方法は何通りありますか。

上の2問の違い、わかりますか？

大切なのは、順番が重要かどうかです。

 

解説

(1)5人の生徒をA、B、C、D、Eと置きます。
たとえば、「Aが会長でBが副会長」というケースと「Bが会長でAが副会長」というケースは区別しなければいけません。

会長を決めて、副会長を決める。連続して起こることはかけ算でしたね。
よって、5×4＝20通りとなります。

(2)(1)と同様の答えになりそうですが、「Aが1人目の掃除当番でBが2人目の掃除当番」というケースと「Bが1人目の掃除当番でAが1人目の掃除当番」というケースを区別する必要がありません。（掃除当番であれば、1人目でも2人目でも同じですよね？）

よって＝10通りとなります。

のような問題を順列、(2)のような問題を組み合わせと言ったりしますね。

このぐらいなら楽勝！という子！とても心強いです。少し難しくしますよ？

場合の数には様々な問題がありますが、「組み合わせ」を考えてから「順列」を使う、という問題は非常に多いです。実際に見てみましょう。

問題2

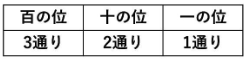
1，2，3，4，5のカードが1枚ずつあります。この5枚のうち、3枚を並べて3けたの数を作ります。3の倍数になるようなカードの並べ替え方は何通りありますか。

 

解説

まずは順番を気にせず、使用するカードの和が3の倍数になるように組み合わせから考えましょう。また、ここで「場合分け」という考え方が出てきます。
使用するカードが１～5なので、和は1＋2＋3＝6から3＋4＋5＝12までのどれかになります。ということは、以下の3パターンが考えられます。

(ⅰ)和が6

(1,2,3)

(ⅱ)和が9

(1,3,5)
(2,3,4)

(ⅲ)和が12

(3,4,5)

これだけあります。漏れの無いように注意しましょう。

さて、このあと選んだカードを並べ替えていきます。順列ですね。

たとえば(1,2,3)のカードだと・・・・

3×2×1＝6通りになります。さあ、あと一歩です。

組み合わせは4通りありました。

よって、6×4＝24通りとなります。

組み合わせを考えてから順列を考える、という手順、納得できますか？

もう1問いきましょう。

問題3

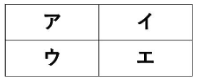
下の図の形を赤、青、黄、緑の4色の絵の具でぬり分けます。使わなくていい色があってもよいものとすると、全部で何通りのぬり方がありますか。

 

解説

色のぬり分けに関する問題です。ぬる場所が4か所ありますが、隣り合う箇所を別の色でぬることを考えると最大で4色、最小で2色必要となります。それぞれの場合について、必要に応じて、組み合わせを考えてから順列の計算を行っていきましょう。

(ⅰ)4色でぬり分ける場合

4×3×2×1＝24通りです。ここは大丈夫なはず！

(ⅱ)3色でぬり分ける場合

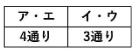
アとエを同じ色で塗る場合と、イとウを同じ色で塗る場合の組み合わせがあります。

難しくなってきましたね・・・

それぞれ4×3×2＝24通りあるので、24×2＝48通りです。

(ⅲ)2色でぬり分ける場合

ここを見落とす子が多いかもしれません。
アとエを同じ色で塗り、イとウを同じ色で塗る組み合わせがあります。

4×3＝12通りです。

(ⅰ)～(ⅲ)は同時には起こりません。この場合はたし算でしたね。24＋48＋12＝84通りとなります。

 

ぬり分けは苦手とする子が特に多いように思います。正確な手順を踏むことができるか確認しておくとよいでしょう。

〇順列と組み合わせの違いについて

〇組み合わせを考えてから順列の計算を行う

この2つが今回のテーマでした。

次回は今回もちらっと出てきた「場合分け」の考え方について触れる予定です。

今回の内容がひとつでもお役に立てば幸いです。

それではこれで失礼します。

受験Dr.　川上亮