みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

今回はタイトルの通り、道順の問題を扱いたいと思います。

道順の問題と言えば、以下のようなものが代表的です。

 

【問題①】

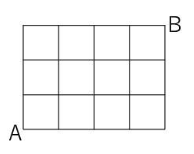
下の図のように直角に交わっている道があります。AからBまで遠回りをしないで行く方法は全部で何通りありますか。

 

【解説】

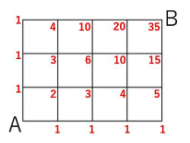
和の法則を用いて、以下のように書き込みを行って解く子が多いのではないでしょうか。

または、組み合わせを利用する方法もありました。

→、→、→、→、↑、↑、↑の並べ替えなので

＝35通りですね。

 

さて、次はやや難し目の問題です。

 

【問題②】

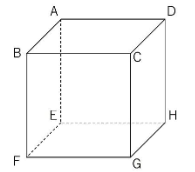
下の図のような立方体があり、点PがAを出発して1秒で次々にとなりの頂点に移動します。AからHまで、4秒で行く方法は何通りありますか。同じ頂点や辺を何回通ってもよいものとします。

 

【解説】

ひとつひとつ道順を確認していくと漏れが出てきてしまいそうです。

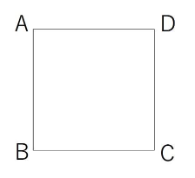
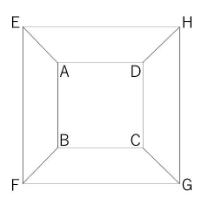
ここで、立方体を上から見た図を描いてみます。

 

真上から見ると下の正方形EFGHが見えないため、EFGHを大きくしましょう。

 

さて、これで準備完了です。

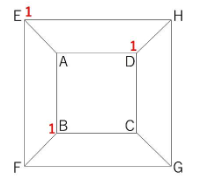
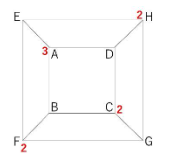
Aから1秒進んで到達できる頂点はB、D、Eの3点です。

 

問題①の道順の問題のように書き込みを行っていきます。

さて、次に進みましょう。

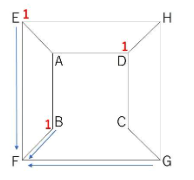
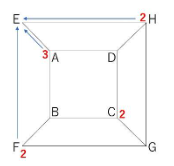
2秒後にFに到達するためには、1秒経ったときにEかBかGのどこかにいる必要があります。Eには「1」、Bにも「1」、Gには数値がありません。
よって、1＋1＝2通りになります。

 

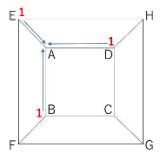
Aについても考えてみます。

2秒後にAに到達するためには、1秒経ったときにB、D、Eにいる必要があります。
よって、1＋1＋1＝3通りですね。

 

同様に、C、Hについて考えましょう。2秒後にCに到達するためには、1秒経ったときにB、D、Gにいる必要があります。

2秒後にHに到達するためには、1秒経ったときにD、E、Gにいる必要があります。

ともに2通りとなります。

さて、これで2秒後の状態が完成しました。

 

3秒後に進みましょう。

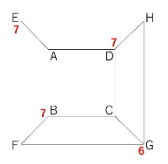
3秒後にEに到達するためには、2秒経ったときにAかFかHのどこかにいる必要があります。Aには「3」、Fには「2」、Hには「2」とあります。

 

3＋2＋2＝7ですね。

同様の手順で3秒後を計算すると以下のようになります。

 

あと一歩。

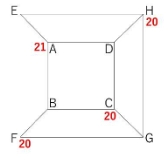
4秒後は以下の状態です。

 

よって、20通りが答えとなります。

立体図形を平面に置き換えること、そして時系列順に道順の問題のように計算することで比較的容易に情報をまとめることができます。

立方体だけでなく、三角すい、四角すいなどでも応用が出来る、おすすめの解法です。
是非活用してみてください。

今回の内容がひとつでもお役に立てば幸いです。

それではこれで失礼します。

受験Dr.　川上亮