みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

今回はタイトルの通り、証明問題についてお話しいたします。

今までも海陽中（特給）や早稲田実業中などで出題されていましたが、2024年度入試においては駒場東邦中でも出題されており、一度は触れておきたい形式の問題です。

今回は2024年度の駒場東邦中の問題を題材に、証明問題の取り組み方のコツをお伝えできればと思います。

問題

①下の図のように、1辺の長さが4㎝の正三角形ABCと1辺の長さが3㎝の正三角形DEFがあり、辺ACと辺DEが交わる点をGとします。三角形AGDにおいて、角Aの大きさが30°のとき、三角形AGDと三角形GECの面積の比を最も簡単な整数の比で表しなさい。

②1辺の長さが3㎝の正三角形と1辺の長さが4㎝の正三角形の面積の和は、1辺の長さが5㎝の正三角形の面積に等しいことを①を利用して説明しなさい。

 

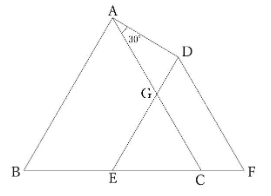
解説

①三角形AGDが「30°60°90°」の直角三角形であるため、AG：GD＝2：1となります。

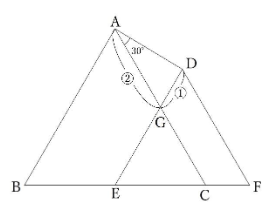
GC＝4－②、GE＝3－①となりますが、三角形GECは正三角形であるため、GC=GEです。
よって、4－②＝3－①より、①＝1となります。これを利用すると、辺の長さは以下のようになります。

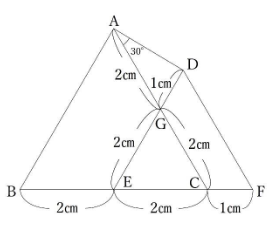
三角形AGDと三角形GECの面積比はAG×GD：GC×GEとなるため、1：2が答えとなります。

②　②がいわゆる「証明問題」です。①を利用して考えていきます。

証明問題のポイント1つ目は「設計図を作ってから取り組む」ことです。要は、問題の題意が本当に成り立つのか、そしてどうして成り立つのかを先に考えておく、ということです。

①で辺の長さを出しました。
BF＝5㎝となっているので、以下のように補助線を引くと一辺5㎝の正三角形が見えてきます。

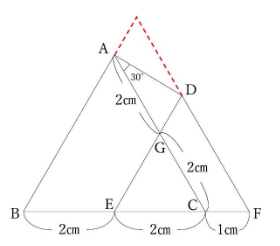
ここで証明問題を解く際のポイント2つ目です。「説明のために必要な点には名前をつける」です。名前が無いと、説明の際に非常に不便です。ここではBAとFDを延長して交わった点をHとします。

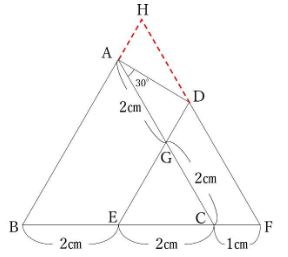
さて、気付きましたか？
三角形AGDと三角形DHAは合同となっています。つまり、三角形DHAの面積も①です。

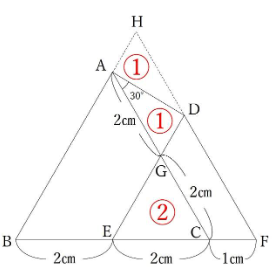
正三角形ABCと正三角形DEFの重なりとなっている正三角形GECと平行四辺形HAGDの面積は等しくなっています。よって、正三角形GECを平行四辺形HAGDに移すことで、題意を満たすことがわかります。

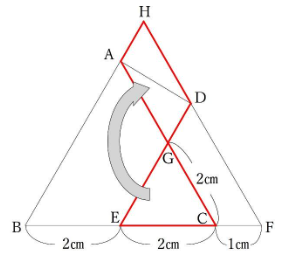
さて、あとは設計図をもとに説明をしていくだけです。

以下、解答となります。

 

解答

BAとFDを延長して交わった点をHとする。
また、三角形AGDと三角形DHAは合同であるため、面積は等しい。
よって①より、三角形GEC＝三角形AGD×2、三角形GEC＝四角形HAGD

また、三角形HBFは1辺5㎝の正三角形
三角形HBF＝三角形ABC＋三角形DEF＋四角形HAGD－三角形GEC
三角形GEC＝四角形HAGDより
三角形HBF＝三角形ABC＋三角形DEF
よって1辺の長さが3㎝の正三角形と1辺の長さが4㎝の正三角形の面積の和は、1辺の長さが5㎝の正三角形の面積に等しい。

 

ポイント①　設計図を作ってから取り組む
ポイント②　説明のために必要な点には名前をつける

ご参考になる点があれば幸いです。

それでは、今回はここで失礼します。

受験Dr.　川上亮