みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

今回はタイトルにある通り、問題の解法を複数備えておくことの重要さについてお話しいたします。受験生だけでなく、小4・小5のお子様にも自信を持ってお伝えできる内容になります。

解き方が1つしかないと、問題によっては非効率になってしまったり、時間がかかりすぎてしまいます。
頭の柔らかい皆さんは、同じ問題でも複数の解法を備えておきましょう。必ず役に立ちます。

さっそく問題です。

問題１

1～100までの整数の中があります。2の倍数と3の倍数を取り除いていくと、何個の整数が残りますか。

 

解説1

ベン図を解法として選択する子が多いのではないでしょうか。

100÷2＝50
100÷3＝33・・・1
100÷6＝16・・・4

より、以下のようになります。

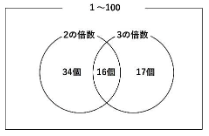
100－（34＋16＋17）＝33より、答えは33個となります。

では、次の問題だったら、どう解きますか？

 

問題2

1～100までの整数の中があります。

(1) 何個の整数が残りますか。
(2) 残った整数のうち、小さいほうから数えて21番目の数はなんですか。

違いは(2)の有無ですね。この問題、ベン図で解くのはとっても損です。

 

解説2

(1)1～6までを1周期とする。

2の倍数と3の倍数を取り除くと、1と5の2個になります。

100÷6＝16・・・4より、16グループと4個の数があるので

2個×16グループ＋1＝33個となります。

(2)ここで、(1)を周期で解いたことが活きてきます。

残った数を小さい順に並べ、グループ分けします。

21番目の数は、21÷2＝10・・・1より、11グループの1番目の数となります。

よって、6×10＋1＝61となります。

この(2)、ベン図で解くことは難しいです。それなら最初から周期を利用しよう、ということです。

大問全体を見てから解法を選ぶことを意識しましょう。

他にも複数の解法を備えておくことで解くスピードが大きく変わるおまけ問題を紹介しておきます。（小6のお子様向けです）

 

おまけ

下の図のような山道を、A地点からB地点に行くのに21分、B地点からA地点に行くのに19分かかります。上りは分速60m、下りは分速90mで移動します。

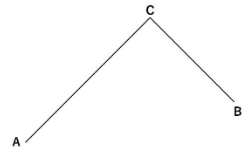
(ア)AC間の距離を求めなさい。
(イ)AB間の距離を求めなさい。
(ウ)AC間はBC間より何m長いですか。

それぞれ独立した問題として考えてみてください。
効率の良い解法が選択できでいますか？

是非チャレンジしてみてください。
念のため、解答とポイントを下に記しておきます。

 

 

 

 

 

 

 

 

解答

(ア)900m
(イ)1440m
(ウ)360m

 

ポイント

（１）距離一定の考え方を使いましょう。

上りと下りの速さの比は60∶90＝2∶3なので、AC間を移動する時間の比は3∶2です。BC間でも同様です。

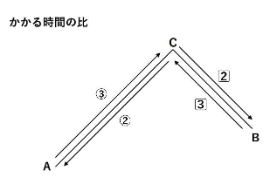
あとは時間に関する消去算を利用して・・・という流れになります。

(１)（ア）と似ていますが、上りには40×＝24分、下りには40×＝16分かかっている

ことを利用するとスピーディーに処理できます。

(ウ)CD＝BCとなる地点DをAB上にとります。

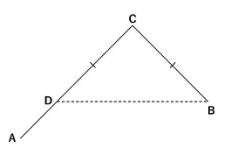
AD間で距離一定の考え方を使うと、上りと下りでかかる時間の比は3：2です。

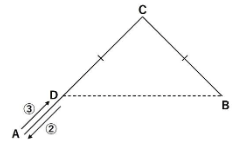
この区間で行きと帰りの時間の差が生まれることを考慮すると
③－②＝21－19
より、①＝2分とわかります。

いかがでしたでしょうか。
様々な解法に触れ、自分の中に落とし込むことが長い目で見たときに必ず役に立ちます。

ご参考になる点があれば幸いです。

それでは、今回はここで失礼します。

受験Dr.　川上亮