みなさん、こんにちは。
受験Dr.算数・理科科の川上と申します。

今回はタイトルの通り、立体の共通部分を考える問題に触れていきたいと思います。難関校を中心に出題が増えており、個人的に注目している題材です。

 

問題

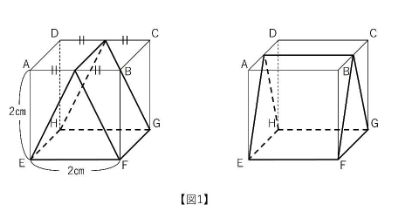
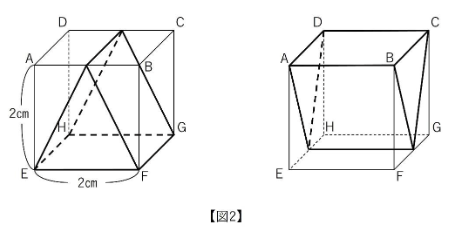
底辺が2㎝で高さが2㎝の二等辺三角形を底面とする、高さ2㎝の三角柱を考えます。この三角柱を以下の図のように１辺の長さが2㎝の立方体ABCD-EFGHの中に置きます。

(1)図1のように、三角柱の向きを変えて2通りの置き方をしました。これらの共通部分の立体Xの体積を答えなさい。（栄光学園中2024　一部抜粋・表現変更）

 

解説

立体の共通部分を考える問題は、あらゆる立体図形の知識・解法を組み合わせて対応します。この問題は「複数回切断」の解法と共通点があります。

というのも、図1の2つの立体は立方体から三角柱を2つ切断し、取り除いた立体だからです。（下の図の赤線で表された三角柱を取り除きます）

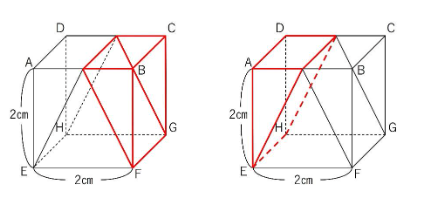
さて、複数回切断では「交線の作図」がポイントでした。切断面の交線を結んでみましょう。

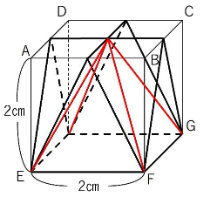
下の図のような四角すいが見えますでしょうか。

体積は㎤　となります。

2問目に行きましょう。

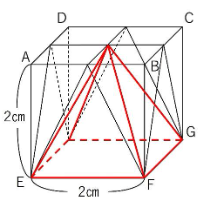
(2)図2のように三角柱の向きを変えて2通りの置き方をしました。これらの共通部分の立体Yの体積を答えなさい。

これも「交線の作図」がポイントですね。
以下の三角すいが作図できればカンペキです。

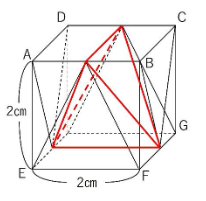
高さの平均を使用しましょう。
図の青の三角形を底面と見ます。

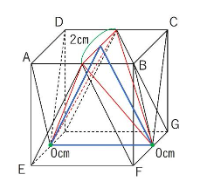
底面に対する高さはそれぞれ2㎝、0㎝、0㎝です。（下の図の緑色をつけたところが高さになります）

㎤　となります。

余談ですが、立体の切断＆求積において、高さの平均を使いこなせる子が毎年少ないように思います。今回のように、角出しで対応出来ない場合も想定して、解法を複数備えておくとよいですね。

さて、最後です。

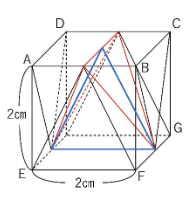
(3) 図3のように三角柱の向きを変えて2通りの置き方をしました。これらの共通部分の立体Zの体積を答えなさい。

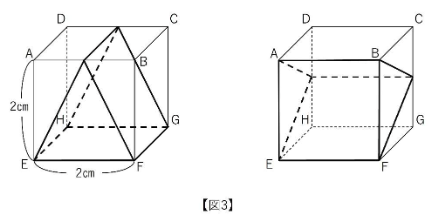
さて、これも「交線の作図」です・・・が、かなり見づらいかもしれません。

以下のような四角すいが描けましたか？

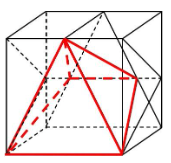
あとは体積ですね。これも角出しは難しそうです。高さの平均で対応しましょう。
下の図の青色を付けた部分の三角形を底面と見ます。

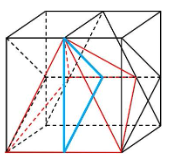
高さは2㎝、1㎝、0㎝ですね。（下の図の緑色の部分です）

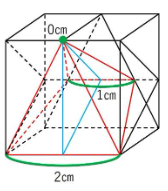
㎤　となります。

いかがでしたでしょうか。
立体の共通部分を考える問題は難問が多く、以前の私は捨て問扱いにすることが多かったです。しかし、出題が増えてきたため、そうも言っていられないなぁ・・・と考えるようになりました。

まずは土台となる「立体切断のルール」「複数回切断」「高さの平均による求積」などをおさえ、過去問等で取り組み、対策を行っておきましょう。

ご参考になる点があれば幸いです。

それでは、今回はここで失礼します。

受験Dr.　川上亮