みなさんこんにちは、受験ドクターの久米です。
今回は算数が苦手なお子さんのため、
「場合の数」を表で解く方法をお話しします。

算数が苦手なお子さんは、抽象的思考があまり好きではない傾向にあります。
模範解答の式だけを見てもイメージが湧かず、
式が何を意味しているのかピンとこないことが多くあります。
そういうお子さんには実際にどうなっているのかを書いてみせるのが一番です。
実際に書き出すやり方としては樹形図が有名ですが、
今回はサイコロ問題のときに有効な「表」の書き方をお話しします。

例題1
1つのサイコロを2回振るとき、
1回目に出た目と2回目に出た目の差が2になるのは全部で何通りですか。

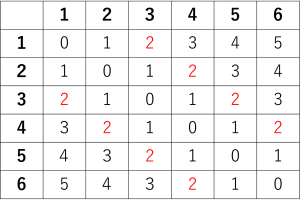
まず下のような表を書きます。

その後で、差の数字を入れていきます。

図の赤いところを数えると、答えは8通りになります。

例題2
1つのサイコロを2回振るとき、積が偶数になるのは全部で何通りですか。

今度は数字を全部書くのではなく、当てはまるところを塗りつぶす方法でやってみます。
奇数×偶数=偶数、偶数×奇数=偶数、偶数×偶数=偶数になるので、
下の表のようになります。

図の赤いところを数えると、答えは27通りになります。
（奇数×奇数=奇数となるので、図の白いところを数えて36-9=27通りという解き方もあります）

例題3（桐光学園2014改題）
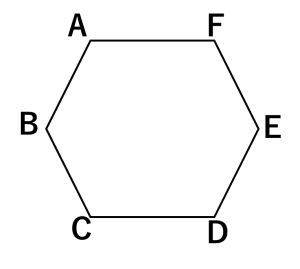
下図のような正六角形ABCDEFがあります。

1つのサイコロを投げ、出た目により、点Pは次の規則①②にしたがって、
正六角形の1つの頂点から次の頂点に進みます。
①１，２，３の目が出たら、出た目の数だけ反時計回りに進みます。
②４，５，６の目が出たら、出た目から３引いた数だけ時計回りに進みます。
サイコロを２回投げたとき、点Pが頂点Dに止まるようなサイコロの目の出方は何通りですか。

表を書いて解いていきます。
上と同様の表を書くと、下のようになりますが…

今回の問題では、123の目の動き方と、456の目の動き方が違うので、
上の表を使うと作業にものすごく時間がかかってしまいます。

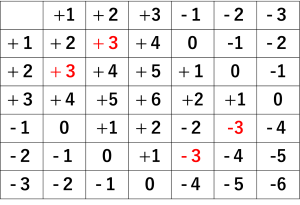
出た目ではなく、動きを表にしてみます。
反時計回りを＋1,＋2,＋3
時計回りを－1,－2、－3とします。

点Dは点Aから+３または-３の場所にあるので。
答えは赤字の4通りとなります。

表整理の利点と欠点は以下のようになります。
利点…①見やすい　②書き漏れを起こしにくい　③難問でも簡単な問題でも同様に解ける
欠点…①簡単な問題のときに時間がかかる　②表を書くのが面倒
サイコロ問題が苦手なお子さんは、今回の表の解き方を取り入れてみてください。

それではまた。受験ドクター、久米でした。