みなさんこんにちは、受験ドクターの久米です。
今回も前回に引き続き、「場合の数」を表で解く方法をお話しします。
 
 
表で解くことの利点と欠点は以下の通りです。
利点…①見やすい　②書き漏れを起こしにくい　③難問でも簡単な問題でも同様に解ける
欠点…①簡単な問題のときに時間がかかる　②表を書くのが面倒
パターンが良く分からないとき、式のイメージが出来ないとき、
表整理は有効な手段となります。
今回はやや難しめのサイコロ問題を表で解いていきます。
 
 
例題1（フェリス女学院2019改題）
白色、黄色、赤色のサイコロがそれぞれ1個ずつあります。
この3個のさいころを同時に投げます。
どの2個のさいころの出る目の差も4以下となるような目の出方は何通りですか。

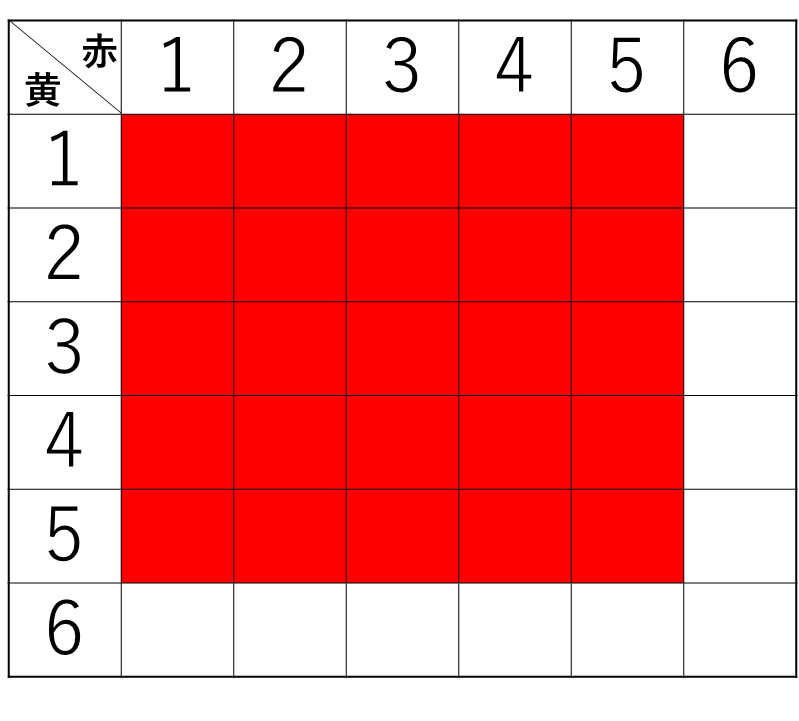
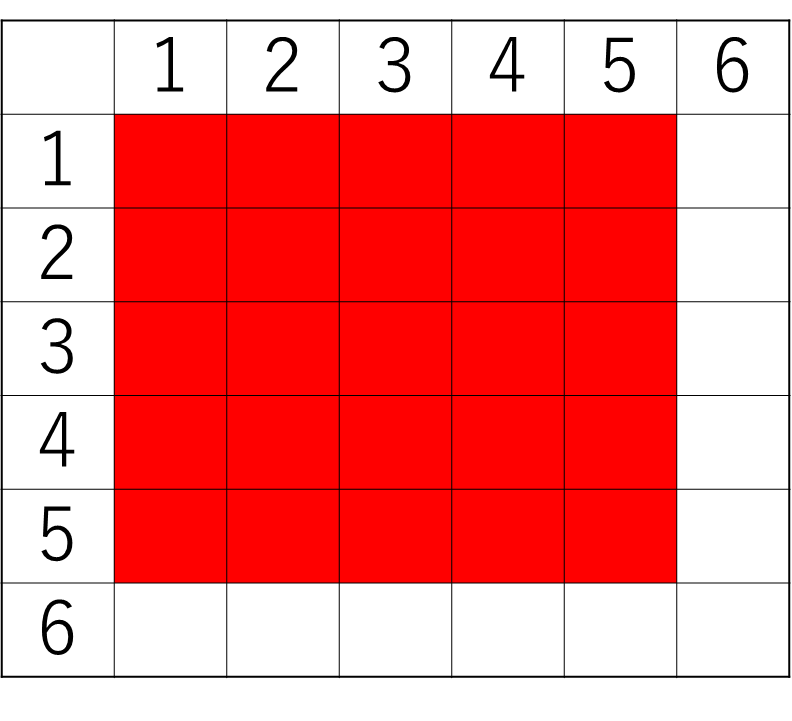
白=1の目が出たときの表を書いてみます。

赤と黄は6が出なければよいので、
下の表の赤い部分が条件を満たします。
したがって、白=1のときは25通りです。

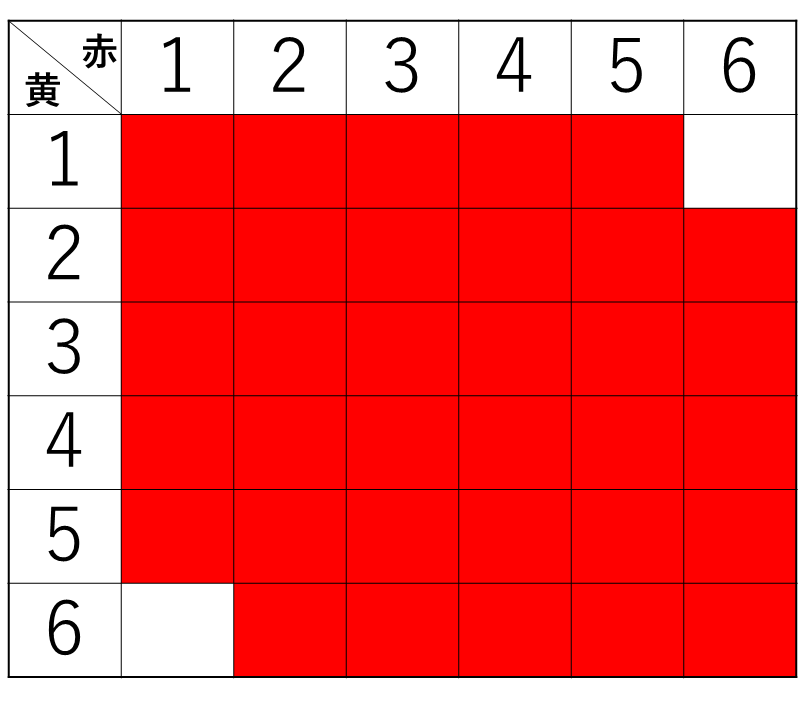
同様に、白=2のときの表を書いてみます。

赤と黄が１と６または６と1の場合だけダメなので、赤い部分が条件を満たします。
したがって、白=2のときは34通りです。

白=3のときを書いてみます。

あれ？白=2のときと3のときの表は同じになりますね。
白=4のとき、白=5のときも白=2のときと同じになります。
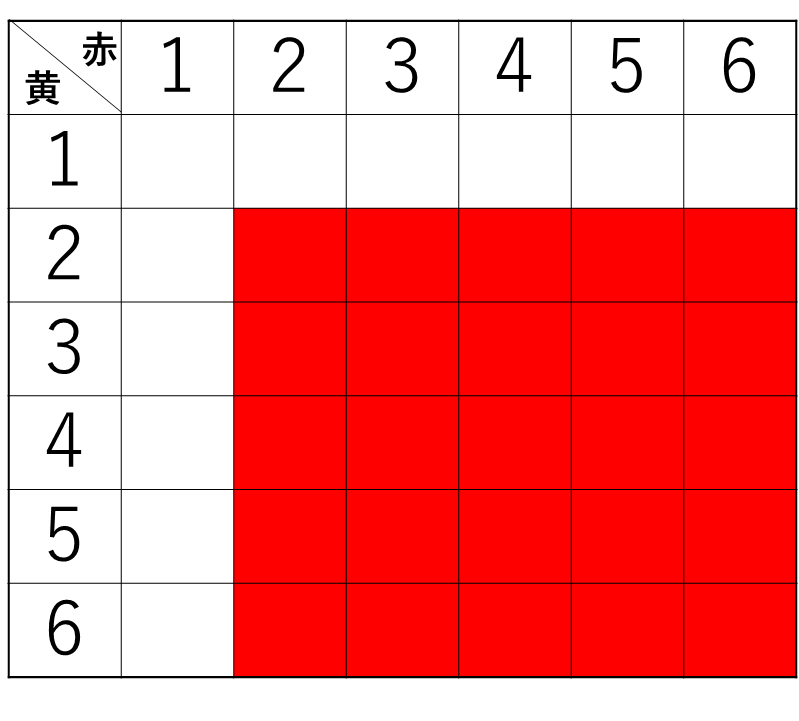
白=6のときは、下のようになります。

点対称ですが、白=1のときと同様ですね。
白=１のとき25通り
白=2のとき34通り
白=3のとき34通り
白=4のとき34通り
白=5のとき34通り
白=6のとき25通り
全部で25×2+34×4=186通りとなります。
 
 
例題2（フェリス女学院2019改題）
白色、黄色、赤色のサイコロがそれぞれ1個ずつあります。
この3個のさいころを同時に投げます。
出る目の最も大きい目が5であるような目の出方は何通りですか。

例題1と同じ問題の続きです。
白=１のときの表を書いてみましょう。

白=1のときは表より9通りです。
白=2のとき、白=3のとき、白=4のときは全て白=1のときと同様です。
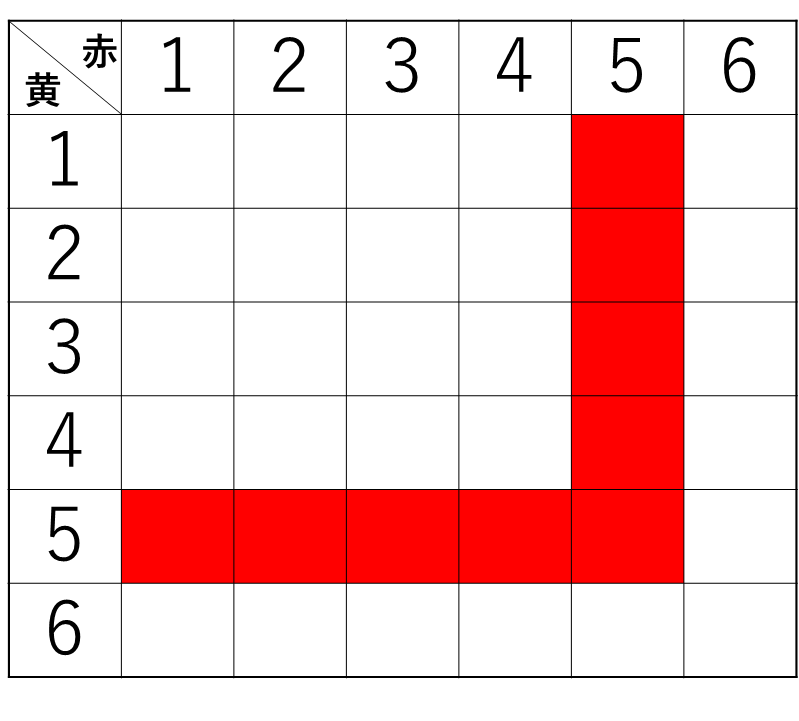
白=5のときは、下のような表になります。

白=5のときは、６さえ出なければOKです。
したがって、白=5のときは25通りです。
白=6のときは、5以下という条件にあてはまりません。
白=１のとき9通り
白=2のとき9通り
白=3のとき9通り
白=4のとき9通り
白=5のとき25通り
白=6のとき0通り
全部で9×4+25=61通りとなります。
 
 
書き上げる方法としては樹形図の方がポピュラーですが、
例題1で出てきた「25通り」「34通り」を樹形図で縦に並べて書くには訓練が必要です。
表ならば、どんな人でもたくさんの数を見やすく並べて書くことが可能です。
表の書き上げをマスターすれば、心強い武器になってくれるでしょう。

それではまた。受験ドクター、久米でした。