みなさんこんにちは。受験Dr.の久米です。
今回は中学受験算数でよく出題される、半径の分からない円の問題についてお話しします。
まず、一般的な解法を紹介してから、私がお薦めする面積比を使った解法をお伝えします。
例題1(一般的な解法=□×□を使った解法)
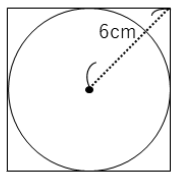
下の図は正方形と円からできている図形です。
円周率を3.14としたとき、円の面積は何㎠ですか。
一般的な解法では、円の半径を□㎝として、
□は分からなくとも□×□の積が出せることを使って解いていきます。
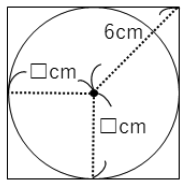
円の半径を□㎝とおきます。
□㎝の長さは分かりませんが、□×□の面積はこの正方形の1/4です。
正方形の面積は対角線×対角線÷2で出せるので、
6×2=12㎝…正方形の対角線
12×12÷2=72㎠…正方形の面積
72÷4=18㎠…□×□の面積
したがって、□×□=18ということが分かります。
この円の面積は□×□×3.14で出せるので、
18×3.14=56.52㎠
次に面積比を使った解法の基本となる考え方を紹介します。
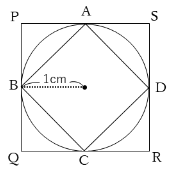
例題2(面積比を使った解法の基本)
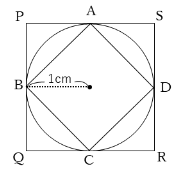
下の図は正方形2つと円からできている図形です。
大きい正方形の面積と円の面積と小さい正方形の面積をそれぞれ求めなさい。
大きい正方形は一辺の長さが1×2=2なので、
2×2=4㎠…大きい正方形の面積
1×1×3.14=3.14㎠…円の面積
正方形の面積は対角線×対角線÷2で出せるので、
1×2=2㎝…小さい正方形の対角線の長さ
2×2÷2=2㎠…小さい正方形の面積
以上のことから、大正方形と円と小正方形の面積比は4:3.14:2であることが分かりました。
比を書くときには一番簡単な整数比にすることが基本ですが、
今回は覚えやすさを優先してあえて小数を使った比の形にしています。
この4:3.14:2の比を使うと、問題を簡単に解くことができます。
また、面積比の数字が暗記できず分からなくなったときでも、
半径1㎝の円と正方形を書けばその場で比を求めることができますので、
完璧に暗記しなくても大丈夫なのがこの解法のいいところです。
例題3(面積比を使った解法)
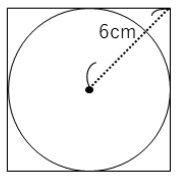
下の図は正方形と円からできている図形です。
円周率を3.14としたとき、円の面積は何㎠ですか。
例題1と同じ問題を、面積比を使った解法で解いてみます。
正方形の面積は上と同じように考え、72㎠。
大きな正方形と円の面積比は4:3.14なので、
正方形の面積は、72÷4×3.14=56.52㎠
やっていることは一般的な解法と同じですが、
□×□を使わないぶん、すっきりとした式になっています。
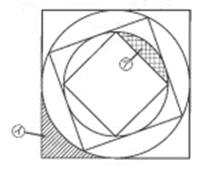
例題4(面積比を使った解法の発展)
下の図は正方形と円からできている図です。
図の㋐の部分が57㎠のとき、㋑の部分は何㎠ですか。
(2021年度1次 渋谷教育学園渋谷)
この問題は一見難しい問題ですが、今回の面積比の考え方を使えば簡単に解けます。
一番大きな正方形を大正方形、次の正方形を中正方形、一番小さい正方形を小正方形、
大きい円を大円、小さい円を小円として連比を出します。
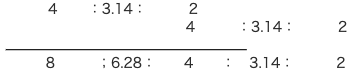
(円の外部の正方形)と(円)と(円の内部の正方形)の面積比は4:3.14:2なので、
大正方形:大円:中正方形:小円:小正方形
㋐の面積比は(3.14-2)÷4=0.285…これが57㎠
57÷0.285=200㎠…比の1
㋑の面積比は(8-6.28)÷4=0.43
㋑の面積は200×0.43=86㎠ となります。
□×□の計算を何度も行うのが面倒な場合、
面積比の考え方を使うと、早く正確に解くことができます。
下の図の大正方形と円と小正方形の面積比は4:3.14:2ということを覚えて、
半径の分からない円の問題に積極的に使っていきましょう。
それではまた。受験Dr.久米でした。