みなさんこんにちは。受験Dr.の久米です。
今回は前回・前々回に引き続き、単位の問題です。
その中の縮図計算について学習しましょう。
縮図計算は、できる人とできない人の差がつきやすい分野です。
今回は、縮図計算が苦手な人でも理解できるように、考え方の根本をお話しします。

まずは長さだけ考えればよい、簡単な例題を2つやってみましょう。

 

例題１

縮尺の地図上で4㎝の長さは、実際には何ｍですか。

 

解答

地図を実際の長さに戻すと大きくなりますから、25000倍になります。

4㎝を25000倍するので、4㎝×25000＝100000㎝＝1000ｍ

 

例題２

実際の長さが400ｍのとき、の地図上では何㎝ですか。

 

解答

実際の長さを地図にすると小さくなりますから、になります。

単位を解答にそろえるためmを㎝にすると400ｍ＝40000㎝、
それをするので、
40000㎝×＝1.6㎝

例題1と2から、長さの場合は、25000やを1回だけかけ算することが分かります。

次に、面積を考える例題を2つやりましょう。

 

例題３

の地図上で、たての長さ4㎝、横の長さ5㎝の長方形の土地があります。

実際の面積は何㎢ですか。

 

解答

たての長さは4㎝×25000＝100000㎝＝1000ｍ＝1㎞
横の長さは5㎝×25000＝125000㎝＝1250m＝1.25㎞

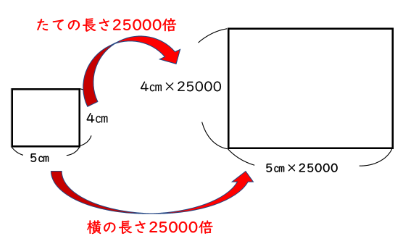
実際の面積は1×1.25＝1.25㎢

 

例題4

実際の長さがたて1000ｍ、よこ500ｍの長方形の土地は、
の地図上で何㎠の面積になりますか。

 

解答

1000ｍと500ｍをそれぞれにします。
解答の単位にそろえるため、ｍをcmにします。
1000m=100000㎝なので、100000×＝4㎝…地図上のたての長さ
500m=50000㎝なので、50000×＝2㎝…地図上の横の長さ

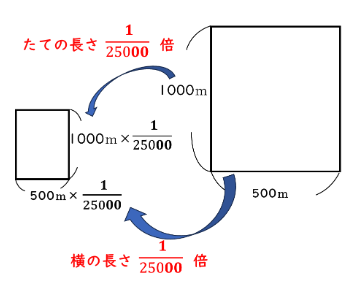
地図上の面積は4㎝×2㎝＝8㎠

例題3と4から、面積の場合は、25000やを２回かけ算することが分かります。

それでは、具体的な長さが出ていない面積の問題をやりましょう。

 

例題５

の地図上で20㎠の面積の土地は、実際の面積は何㎢ですか。

例題5では解き方を2つ紹介します。
解答①は、実際の長さにあてはめて解くやり方です。
縮図の問題が苦手だ、というお子さんはこの解き方をまず覚えましょう。

解答②は、塾のテキストや参考書に載っている一般的な解き方です。
数字がたくさん並んでいて意味が分かりにくいので、
解説でその式の意味を解説します。

 

解答①（たての長さと横の長さをあてはめて考える解き方）

20㎠なので、かけ算して20になるように、たての長さと横の長さを決める。
20＝4×5なので、たて4㎝、横5㎝とすると、
例題３と同じように考えることができます。

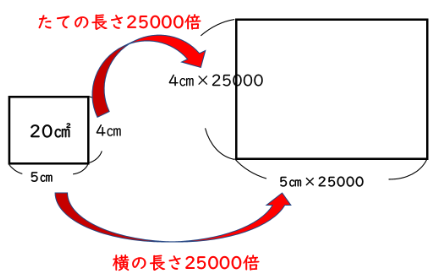
たての長さは4㎝×25000＝100000㎝＝1000ｍ＝1㎞
横の長さは5㎝×25000＝125000㎝＝1250m＝1.25㎞
実際の面積は1×1.25＝1.25㎢
（今回は20㎠の面積を「たて4㎝、横5㎝の長方形」と考えて解きましたが、
20㎠の面積を「たて2㎝、横10㎝の長方形」と考えても、
「たて1㎝、横20㎝の長方形」と考えても、
答えは同じ1.25㎢となります）

 

解答②

20㎠×25000×25000÷（100×100×1000×1000）＝1.25㎢

 

解説

地図上の面積を実際の面積にするときには、たてを25000倍、横を25000倍する必要があります
20㎠×25000×25000÷（100×100×1000×1000）＝1.25㎢
上記の赤字部分は、地図上の面積から実際の面積を出しています。
次に、面積の単位を㎠から㎡に変えます。
1㎡＝1ⅿ×1ⅿ＝100㎝×100㎝なので、
100㎝×100㎝＝1㎡となります。
20㎠×25000×25000÷（100×100×1000×1000）＝1.25㎢
上記の赤字部分は、面積の単位を㎠から㎡に変えています。
次に、面積の単位を㎡から㎢に変えます。
1㎢＝1㎞×１㎞＝1000ⅿ×1000ⅿなので、
1000ⅿ×1000ⅿ＝1㎢となります。
20㎠×25000×25000÷（100×100×1000×1000）＝1.25㎢
上記の赤字部分は、面積の単位を㎡からhaに変えています。
解答②の式を分数の形で表すと、以下のようになります。

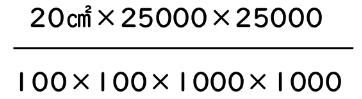
この式を約分すると答えとなる1.25㎢が出ます。

最後に、実際の入試問題をやりましょう。

 

例題6

の縮尺の地図で10㎠の面積の土地は、の縮尺の地図では□㎠です。
（国学院久我山2024）

の地図との地図では、の地図の方が大きいです。
25000÷10000＝2.5なので、たての長さと横の長さがどちらも2.5倍になると考えます。

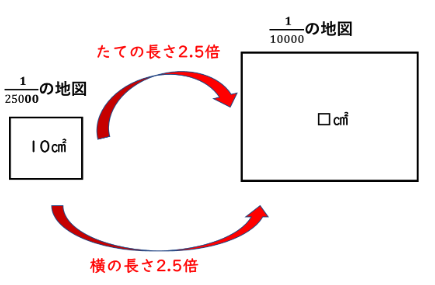
10×2.5×2.5＝62.5㎠

この問題は合格者の正答率は男子70.3％、女子63.6％でしたが、
不合格者も含めた全体の正答率は男子43.9％、女子39.9％でした。
合否を分けた問題と言えるでしょう。

例題5の解答②のやり方を丸暗記しただけでは解けません。
しかし、面積の大きさの根本原理を理解し、図をイメージすれば簡単に解けます。

それではまた。受験Dr.久米でした。