みなさんこんにちは。
受験Dr.の久米です。

今回は算数の「集合算」についてお話しします。
集合算とは、下のような問題です。

例題1

ある学年の生徒に通学手段と通学時間についてのアンケートを行いました。
アンケートは「はい」か「いいえ」のどちらかで解答してもらいました。
「通学手段に電車を使いますか」という質問に、「はい」と答えた人は全体の84％で、
「通学時間は45分未満ですか」という質問に「はい」と答えた人は全体の80％でした。
また、通学手段に電車を使わず、通学時間が45分以上の生徒の人数は6人でした。
生徒全体の人数は300人です。
通学手段に電車を使い、通学時間が45分未満の生徒は何人ですか。
（立教池袋2023　改題）

例題1の質問は「電車を使いますか」「通学時間は45分未満ですか」の2種類、
答えは「はい」「いいえ」の2種類です。
ですから、例題1は「質問が2つ、答え方が2つ」の問題といえます。
このような集合算の解き方は大きく分けて３つあります。
①表整理
②ベン図
③線分図

それぞれの整理の仕方は以下の通りです。

①表整理の場合

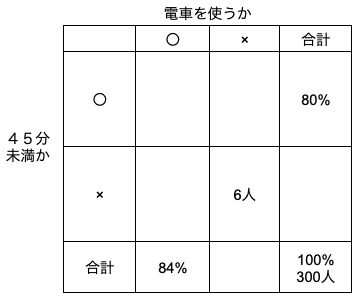
表の縦で通学時間の質問に対する答えを区分し、
表の横で電車を使うかの質問に対する答えを区分しています。

②線分図の場合

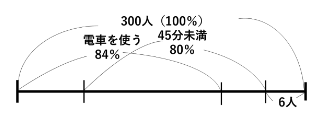
線分に含まれるかどうかでそれぞれの質問に対する答えを区分しています。

③ベン図の場合

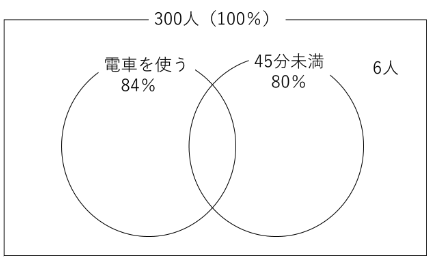
〇の数が質問の数で、
〇の内部にあるか外部にあるかで質問に対する答えを区分しています。

①②③すべてに共通する区分の仕方は以下の通りです。
「質問Aの答え方×質問Bの答え方＝区分の方法」
例題1は、全体を2×2＝4つに区分する問題と考えられます。
細かい解き方は省略しますが、①②③のどの方法を使っても解くことができます。
（答え　198人）

それでは、別の区分の仕方をする問題に行きましょう。

例題2

ある学校の生徒60人に、犬についてのアンケートをとったところ、
「好き」が32人、「きらい」が18人、「好きでもきらいでもない」が10人でした。
また、同じ生徒にねこについてのアンケートをとったところ、
「好き」が30人、「きらい」が21人、「好きでもきらいでもない」が9人でした。
また、この2回のアンケートで、最低1回は「好きでもきらいでもない」と
答えた生徒は15人でした。
⑴両方とも「好きでもきらいでもない」と答えた生徒は何人ですか。
⑵一方に「好き」、他方に「きらい」と答えた生徒は22人でした。
また、一方に「好き」、他方に「好きでもきらいでもない」と答えた生徒は8人でした。
①両方とも「好き」と答えた生徒は何人ですか
②両方とも「きらい」と答えた生徒は何人ですか。
（桐朋　2011）

この例題2、どの方法で解けばよいのでしょう？
例題2の質問は「犬について」「ネコについて」の2種類、
答え方は「好き」「きらい」「どちらでもない」の3種類です。
したがって、今回の例題2は「質問が2つ、答えが3つ」の問題となりますから、
「質問Aの答え方3種類×質問Bの答え方3種類＝9つに区分する」必要があります。
線分図でもベン図でも答え方を3つに区分できないので、
今回は表整理の解法を使い、以下のように表を書きます。

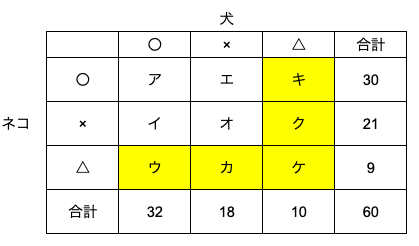
⑴の答えは図のケです。
ケを含む2つの部分の重なりを考えます。
キ+ク+ケ＝10、ウ+カ+ケ＝9
問題文の「最低1回は「好きでもきらいでもない」と答えた生徒15人」が
上の図の黄色い部分（ウ+カ+キ+ク+ケ）の合計なので、
10＋9－15＝4…ケ　⑴　4人

⑵①の答えは図のアです。
⑴同様にアを含む2つの部分の重なりを考えます。

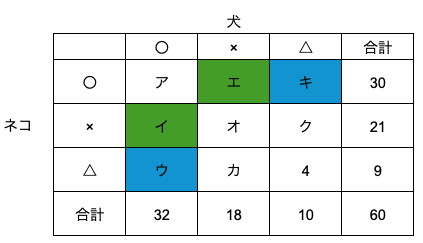
ア＋イ＋ウ＝32、ア＋エ＋キ＝30
「一方に「好き」、他方に「きらい」と答えた生徒22人」が図のイ＋エ、
「一方に「好き」、他方に「好きでもきらいでもない」と答えた生徒8人」が図のウ＋キ
30＋32＝62…アアイウエキの合計
22＋8＝30…イエウキの合計
62－30＝32…アア
32÷2＝16…ア　⑵①　16人

⑵②の答えは図のオです。
これまで同様にオを含む2つの部分の重なりを考えます。

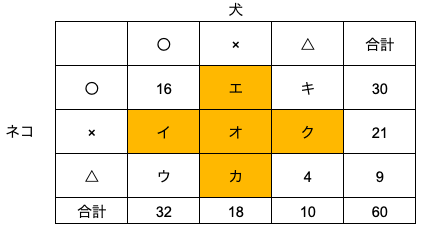
ウ＋キ＝8より、60－（16＋4＋8）＝32…イエオカクの合計
表より、イ＋オ＋ク＝21、エ＋オ＋カ＝18
21＋18＝39…イエオオカクの合計
39－32＝7…オ　⑵②　7人

発展的な集合算の問題は、全体をいくつに区分するかを考えて解きましょう。

それではまた。
受験Dr.、久米でした。