みなさんこんにちは。受験ドクターの桑田です。
4月の講師ブログは、前回の「中学受験生でも解ける!?東大入試 2020年版」の解説編です。
まずは問題の復習から。
問題 2020年東京大学(文科)第2問 大幅に改
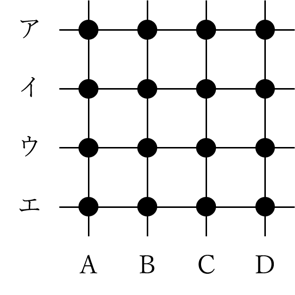
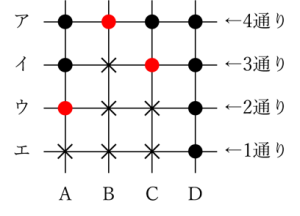
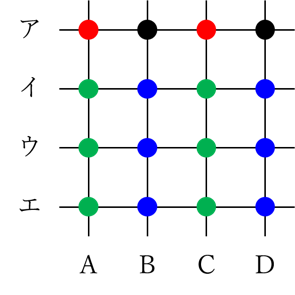
図のように、縦にA~Dの4本の直線を、横にア~エの4本の直線を引き、計16個の交点を考えます。
(1)16個の交点から4個の点を選んだところ、A~D、ア~エの8本の直線すべての上に、少なくとも1個は選んだ点がありました。このような点の選び方は全部で何通りありますか。
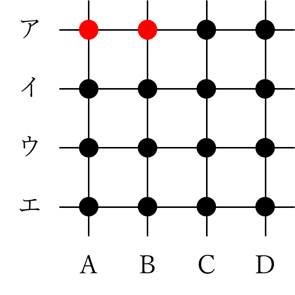
(2)16個の交点のうち、まず、図に赤色で示した2個の点を選びました。残りの14個の交点から、あと3個の点を選び、合計5個の点を選んだところ、A~D、ア~エの8本の直線すべての上に、少なくとも1個は選んだ点がありました。このような点の選び方は全部で何通りありますか。
(3)16個の交点から5個の交点を選んだところ、A~D、ア~エの8本の直線すべての上に、少なくとも1個は選んだ点がありました。このような点の選び方は全部で何通りありますか。
では、解説です!
(1)
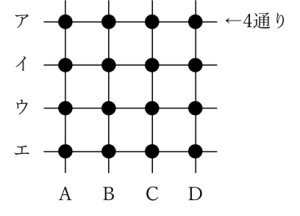
4個の点を選んだ結果、縦、横4本ずつの直線のすべての上に選んだ点があったということから、横に引いたア・イ・ウ・エの直線上には、それぞれ1個ずつの点が選ばれているはずです。
そこで、ア→イ→ウ→エの順に1個ずつ選んでいきましょう。
アの直線上では、4個の点から自由に1個選べるので、選び方は4通り。
その後、イの直線上で点を選ぶときには、アで選んだ点と縦の直線が同じにならないようにする必要があるので、選び方は3通り。
同様に、ウの直線では、すでにアとイで選んだ2点と縦の直線が同じにならないようにするので、選び方は2通り。
そして、エの直線では、ア~ウの直線で選んだ3点のいずれとも縦の直線が同じにならないようにするので、選び方は1通り。
よって、求める場合の数は、4×3×2×1=24通りです。
(2)
いくつかの解法が考えられますが、ここでは前回のヒントに沿って考えてみます。
横に引かれたア~エの直線のうち、アの上にはすでに点が選ばれているので、残りの3点はイ・ウ・エの上に各1個ずつ選ばなくてはなりません。
さらに、縦に引かれた4本の直線のうち、A・Bにはすでに点が選ばれていますが、C・D上にはそれぞれ必ず1点以上選ぶ必要があります。
これを踏まえた上で、あと3個の点を選ぶのに、
①すべてCまたはDの上から選ぶ場合
②1点はAまたはBから選び、あと2点をC・Dから1点ずつ選ぶ場合
の2つの場合に分けて考えます。
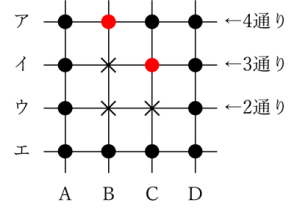
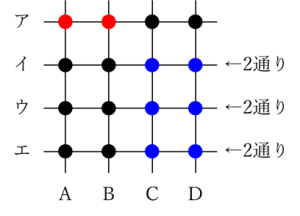
①すべてCまたはDの上から選ぶ場合
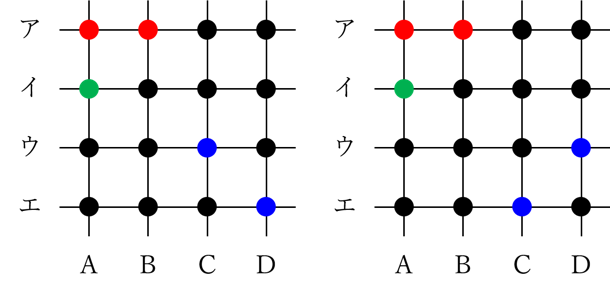
下の図に青く示した6点のうち3点を選ぶことになります。
イ・ウ・エの直線上に各1点ずつ選ぶ必要があるので、2×2×2=8通りの選び方が考えられますが…。
上に示した2通りの選び方は、縦の直線のうちCまたはD上に点が選ばれていないので条件を満たしません。
よって条件を満たす選び方は8-2=6通りです。
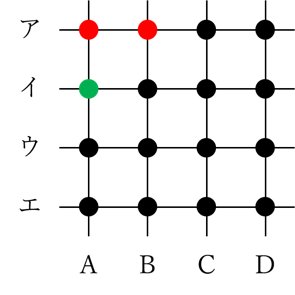
②1点はAまたはBから選び、あと2点をC・Dから1点ずつ選ぶ場合
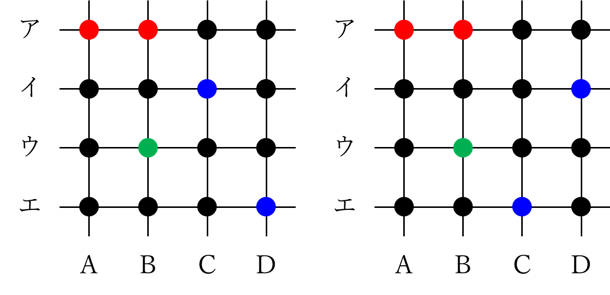
例えば、AまたはBから選ぶ1点を、下の図に緑色で示した点にしたとしましょう。
さて、残りは2点。条件を満たす選び方は何通りあるでしょうか。
横に引かれたウ・エの直線、縦に引かれたC・Dの直線上にまだ点が選ばれていないので、各々1点ずつ選ばれるように点を取らなければなりませんから…。
上の図の青い点のように2通りの選び方が考えられます。
緑色の点の位置を変えたとしても…。
やはり青い点の選び方は2通りあります。
緑色の点は上の図の6点から1つ選ぶことができ、それぞれに対して青い点の選び方が2通りずつあるので、条件を満たす選び方は6×2=12通りです。
①の6通りと②の12通りを合わせ、(2)の答は6+12=18通りです。
(3)
(2)の答をもとにして考えます。
5個の点を選ぶので、横に引かれた4本の直線のうち、1本には2個の点が選ばれ、残りの3本にはそれぞれ1個の点が選ばれています。
(2)では、初めからアの上に2点が選ばれていて、あと3点の選び方を考えました。
その際に…
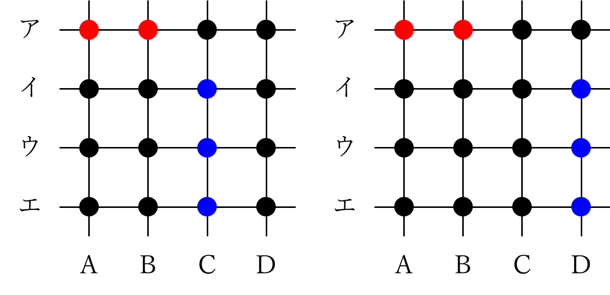
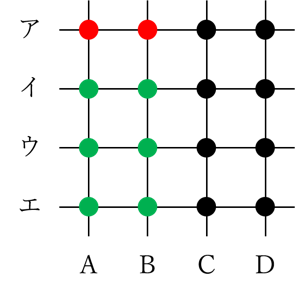
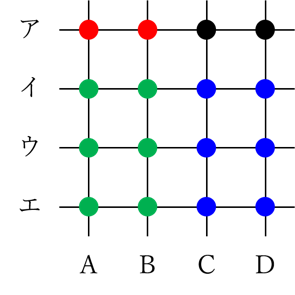
初めから選ばれている赤い2点に対して、上の図のように緑色と青の点に分けてそれぞれの選び方を考えたのでした。
この初めに選ぶ赤い2点を…
このように変えたとしても、緑と青の色分けを上図のようにすれば、(2)と同じように考えて18通りの選び方があることが分かります。
アの上から赤い2点を選ぶ場合の数は、組み合わせの計算を用いて、4×3÷2=6通り。
また、赤い2点をアではなくイ・ウ・エのいずれかの上に選ぶこともできるので、赤い2点の選び方は6×4=24通りあります。
この24通りそれぞれに対して、残り3点の選び方は(2)の18通りずつあるので、(3)の答は18×24=432通りです。
いかがでしたか?
(3)が、2020年東京大学入学試験前期日程 文科の第2問(2)として出題された内容と同等の問題です。
この記事をアップしているのは4月。6年生で場合の数が得意だという受験生でも、まだ難しくてよく分からなかったという人が多いでしょう。
腕に覚えがあるので挑戦してみたいけど、まだ難しいと感じた受験生は、この記事のことを覚えておいて、実力のついた夏から秋にかけて再チャレンジしてみてくださいね。
今回は、ここまで!