みなさん、こんにちは。受験Dr.の桑田陽一です。
11月の講師ブログをお届けします。

今回は、いきなり例題から。

例題

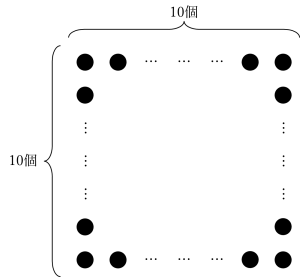
下の図のように、ご石を1辺に10個ずつ、正方形の形に一回り並べました。
並べたご石の数は、全部で何個ですか。

 

「方陣算」の基本的な問題ですね。学習済みの人にとっては簡単だと思います。

もちろん、1辺に10個ずつだから、10×4＝40個！
……ではありませんね。

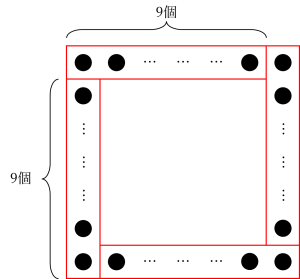
隅のご石を二重に数えないように、1辺のご石より1個ずつ少なく、上の図のように分けるのが最も目にする考え方です。
赤い長方形で囲んだ中には、それぞれ10－1＝9個ずつのご石が入っているので、9×4＝36個が答えです。

何というか、「みんなが少しずつ遠慮すると、世界中が平和に回る」という感じでしょうか。

さて、この「少しずつ遠慮する」という考え方、全然別の単元でも使うことがあります。

例えば…

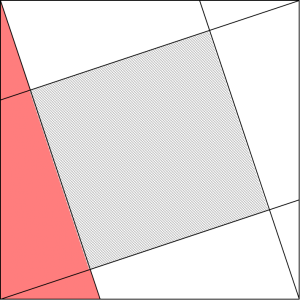
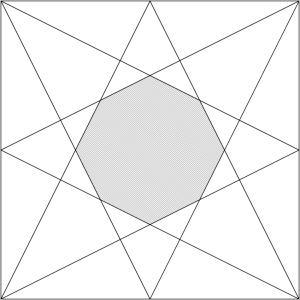
こんな風に、正方形に線を加えた図で、影の部分の面積を求める問題。
学年が進むにつれて、様々な解法を学ぶことになりますが、真ん中の面積を求めるので、今回は全体からまわりの図形を引いて考えることにしましょう。

まわりの図形を考えるときには…

上のような三角形を考えるのではなく、

このように、左下の部分を少しだけ遠慮した赤い三角形を考えてみると、

こうやって、きれいに4つの三角形が組み合わさり、うまく引き算できそうな形になりました！

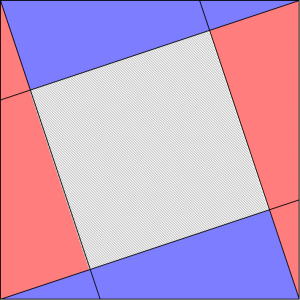
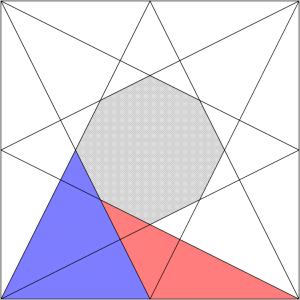
下のような三角形でも…

ここでもまわりの図形の隅っこを譲るように、少しずつ遠慮しあって…

こんな風に組み合わせると良さそうですね。

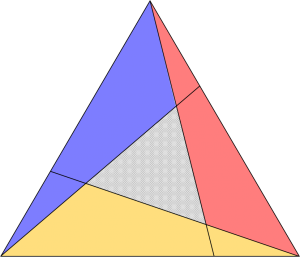
さらには、

少し複雑になりましたが、上の図形はどのように見ると良いでしょうか？

ちょっと工夫して…

このように、2種類の三角形を考えると、見えてきましたか？
…
…
…

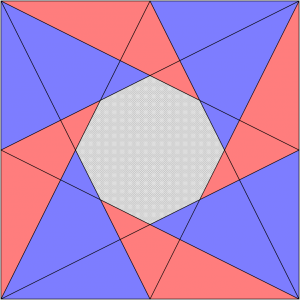
ちょっと目がチカチカしそうですが、やはり4つずつ組み合わせて、全体がうまく収まりました！

6年生や意欲のある5年生は、それぞれの図形に具体的な数値を設定して、実際に影の部分の面積を求めてみると、良い練習になるでしょう。

例えば、最後の図形。
全体の正方形の1辺が6cm、正方形の辺の中点どうしを結んでいるとすると、青い三角形1つの面積は4.5cm^2、赤い三角形1つの面積は3cm^2で、影の部分の面積は、6×6－(4.5＋3)×4＝6cm^2となります。
ぜひ、確かめてみてくださいね。

以上、方陣算で使う「みんなが少しずつ遠慮すると、世界中が平和に回る」という発想を、平面図形の問題でも使える場面があることを見てきました。

方陣算の例題はもちろん、その後の図形の見方も知っていたよ！というみなさん。大変素晴らしいことです！
方陣算の解法と、これらの図形の見方には、似たような発想が使われているよね！というところまで、気がついていたとしたら、もっと立派！

このように、算数や数学には、全く違う単元の問題に見えて、実は同じような発想を使って考えられるようなものが、他にもたくさん埋もれています。
また、機会を見て紹介していきますね。

今回はここまで。